Theory for the Moving Phase Boundary Simulation

It is assumed that local equilibrium holds at the phase interface, i.e. the chemical potentials of all elements are continuous across the boundary, but the chemical potential gradients are in general discontinuous.

In order to maintain mass balance a set of flux balance equations must be satisfied at the phase interface:

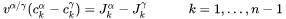
where is the interfacial velocity. The concentrations and the fluxes and 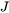are those at the interface on the and 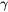sides, respectively.

In the present case there are no degrees of freedom at the interface and the concentrations can be taken directly from a phase diagram. There is only one flux balance equation and the interface velocity can be evaluated once the fluxes at the interface are known. However, for ternary and higher systems the state at the interface must be found by some iterative procedure.

For more information on moving phase boundary problems, see, for example, [1982Ågr], [1992Cru-2], and [1997Hög].

References

[1982Ågr] J. Ågren, Numerical treatment of diffusional reactions in multicomponent alloys. J. Phys. Chem. Solids 43, 385–391 (1982).

[1992Cru-2] S. Crusius, G. Inden, U. Knoop, L. Höglund, J. Ägren, On the Numerical Treatment of Moving Boundary Problems. Int. J. Mater. Res. (Zeitschrift für Met. 83, 673–678 (1992).

[1997Hög] L. Höglund, “Computer simulation of diffusion controlled transformations in multicomponent alloys,” PhD Thesis, KTH Royal Institute of Technology, Stockholm, Sweden (1997).