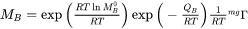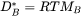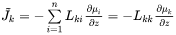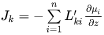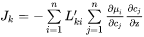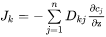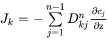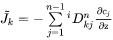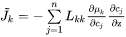Diffusivity Theory
In order to perform simulations using the Diffusion Module (DICTRA), both thermodynamic and kinetic descriptions are needed. Moreover, the results and the accuracy of the simulations critically depend on the quality of these descriptions. So far there is much less kinetic data which has been systematically assessed in the same way as thermodynamic data.
In the theoretical treatment of diffusive reactions one usually works with diffusion coefficients which are evaluated from experimental measurements. In a multicomponent system a large number of diffusion coefficients have to be evaluated, and moreover, they are generally functions of alloy composition and are interrelated. A database would thus be very complex. A superior alternative is to store atomic mobilities in the database, rather than diffusion coefficients. The number of parameters which need to be stored in a multicomponent system are then substantially reduced and the parameters are independent. The diffusion coefficients, which are used in the simulations, can then be obtained as a product of a thermodynamic and a kinetic factor.
The thermodynamic factor is essentially the second derivatives of the molar Gibbs energy with respect to the concentrations, and is known if the system has been assessed thermodynamically. The kinetic factor contains the atomic mobilities, which are stored in the kinetic database. The purpose of this topic is to describe how concentration, temperature and pressure dependence of the atomic mobility can be modeled, as well as to describe relations between the different diffusion coefficients and the atomic mobility.
Modeling of the Atomic Mobility
From absolute-reaction rate theory arguments the mobility coefficient for an element 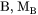 may be divided into a frequency factor
may be divided into a frequency factor 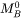 and an activation enthalpy,
and an activation enthalpy, 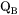 , i.e.
, i.e.
[Eq. 1]
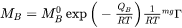
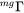 is a factor taking into account the effect of the ferromagnetic transition [Jönsson, 1994a].
is a factor taking into account the effect of the ferromagnetic transition [Jönsson, 1994a]. 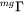 is a function of the alloy composition. It has been suggested by Jönsson, 1994b that one should expand the logarithm of the frequency factor,
is a function of the alloy composition. It has been suggested by Jönsson, 1994b that one should expand the logarithm of the frequency factor, 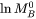 , rather than the value itself, thus the mobility,
, rather than the value itself, thus the mobility,  , is expressed as:
, is expressed as:
Both 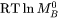 and
and  generally depend upon the composition, temperature, and pressure. In the spirit of the CALPHAD approach [Ågren, 1996], the composition dependency of these two factors, is represented with a linear combination of the values at each endpoint of the composition space, and a Redlich-Kister expansion, viz.
generally depend upon the composition, temperature, and pressure. In the spirit of the CALPHAD approach [Ågren, 1996], the composition dependency of these two factors, is represented with a linear combination of the values at each endpoint of the composition space, and a Redlich-Kister expansion, viz.
[Eq. 3]

where 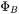 represents
represents 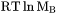 or
or 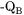 .
. 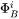 is the value of
is the value of 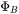 for pure i and thus represents one of the endpoint values in the composition space.
for pure i and thus represents one of the endpoint values in the composition space. 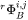 are binary interaction parameters. The commas separate different species interacting with each other.
are binary interaction parameters. The commas separate different species interacting with each other. 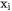 and
and 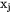 are mole fractions of elements i and j respectively. Each individual
are mole fractions of elements i and j respectively. Each individual 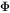 parameter, i.e.
parameter, i.e. 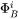 and
and 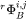 is stored in the database and may be expressed as a polynomial in temperature and pressure, if necessary. The
is stored in the database and may be expressed as a polynomial in temperature and pressure, if necessary. The 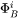 and
and  are referred to in the database as MF and MQ parameters, e.g.
are referred to in the database as MF and MQ parameters, e.g.

is used to represent the frequency factor to the mobility of Cr in pure Ni, i.e.  , whereas:
, whereas:
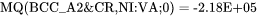
represents 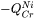 . The magnetic effect is represented by Jönsson's model [1994a].
. The magnetic effect is represented by Jönsson's model [1994a].
[Eq. 4]
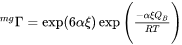
where 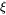 represents the state of the magnetic order (
represents the state of the magnetic order (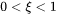 ) at the temperature under consideration and
) at the temperature under consideration and  is treated as a constant, approximately equal to 0.3 in bcc alloys. For fcc alloys the ferromagnetic effect on diffusion is usually neglectable, i.e.
is treated as a constant, approximately equal to 0.3 in bcc alloys. For fcc alloys the ferromagnetic effect on diffusion is usually neglectable, i.e. 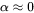 . When there is magnetic ordering it is thus necessary to make the division into MF and MQ because
. When there is magnetic ordering it is thus necessary to make the division into MF and MQ because 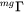 depends on
depends on 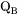 , i.e.
, i.e. 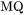 . The full expression then becomes:
. The full expression then becomes:
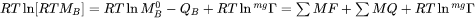
Both MF and MQ may be arbitrary polynomials in temperature and if there is no magnetic effect, i.e. 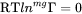 , it is sufficient to enter either one of them. For example, the mobility of Cr in pure Ni may as well be stored as:
, it is sufficient to enter either one of them. For example, the mobility of Cr in pure Ni may as well be stored as:
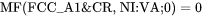
and
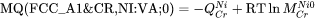
In order to build a database it is necessary to find values on MF and MQ (or when no magnetic effect is considered MQ alone). In many cases such data can be found in the literature. The tracer diffusivity 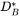 is directly related to the mobility
is directly related to the mobility 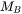 by means of the Einstein relation
by means of the Einstein relation
and when there is no magnetic effect on the mobility, e.g. 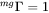 , then from Equation 2 and Equation 5 it is found that:
, then from Equation 2 and Equation 5 it is found that:
[Eq. 6]
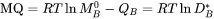
In a more complex database the model parameters are determined from an optimization procedure, where all experimental information is taken into account, see for example Jönsson, 1995 and Engström and Ågren, 1996.
Relationship Between Diffusion Coefficients and Atomic Mobilities
Phenomenological Coefficients
For crystalline phases the vacancy-exchange mechanism of diffusion is predominant, i.e. diffusion occurs by atoms jumping into neighboring vacant lattice sites. From the absolute reaction rate theory, and by assuming that the vacancy concentration is governed by thermodynamic equilibrium, the diffusional flux of a component k in the lattice fixed frame of reference can be expressed as [Andersson and Ågren, 1992]:
Here 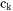 is the amount of k per unit volume,
is the amount of k per unit volume, 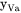 is the fraction of vacant lattice sites on the sublattice where k is dissolved,
is the fraction of vacant lattice sites on the sublattice where k is dissolved, 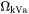 is a kinetic parameter which gives the rate of exchange if there is a vacancy adjacent to a k-atom,
is a kinetic parameter which gives the rate of exchange if there is a vacancy adjacent to a k-atom,
and 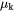 is the chemical potential of component k. The mobility
is the chemical potential of component k. The mobility 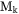 is here defined as:
is here defined as:
[Eq. 8]
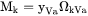 when k is substitutional
when k is substitutional
[Eq. 9]
 when k is interstitial
when k is interstitial
From Equation 7, Equation 8 and Equation 9 it is possible to identify the so called phenomenological parameters that relate the flux of k to all the driving forces, i.e. 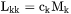 when k is substitutional,
when k is substitutional,  when k is interstitial, and
when k is interstitial, and 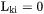 when
when 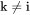 . The fluxes in the lattice-fixed frame of reference may now be expressed as:
. The fluxes in the lattice-fixed frame of reference may now be expressed as:
Transformation to the volume-fixed frame of reference, or the number-fixed frame of reference with respect to the substitutional elements, which may be regarded as the same, if as assumed in the Diffusion Module (DICTRA), the partial molar volumes are independent of concentration, and the partial molar volumes of the interstitials are neglected, yields
where
[Eq. 12]
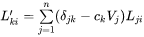
where 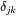 is the Kronecker delta, i.e.,=1 when j=k and 0 otherwise.
is the Kronecker delta, i.e.,=1 when j=k and 0 otherwise. 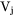 is the partial molar volume of element j.
is the partial molar volume of element j.
Interdiffusion Coefficients
Generally, it is much more convenient to express the fluxes as functions of concentration gradients, rather than gradients in chemical potential. This is accomplished by rewriting Equation 11 using the chain rule of derivation, i.e.
or equally if the unreduced diffusivities,  are introduced,
are introduced,
The 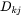 matrix introduced in Equation 14 may be identified by comparing with Equation 13,
matrix introduced in Equation 14 may be identified by comparing with Equation 13,
[Eq. 15]

The 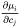 are purely thermodynamic quantities, sometimes they are referred to as thermodynamic factors. It is now evident that the diffusivities may be looked upon as consisting of two separate parts, one purely thermodynamic and one kinetic.
are purely thermodynamic quantities, sometimes they are referred to as thermodynamic factors. It is now evident that the diffusivities may be looked upon as consisting of two separate parts, one purely thermodynamic and one kinetic.
There is a relation between the n concentration gradients in Equation 14 and for practical calculations one usually chooses to eliminate one of them. The reduced diffusivities in a volume-fixed frame of reference, where it is assumed that all the substitutional species have the same partial molar volumes, and furthermore, only the substitutional species contribute to the volume, i.e. the Diffusion Module (DICTRA) frame of reference, is expressed as,
[Eq. 16]
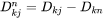 when j is substitutional
when j is substitutional
[Eq. 17]
 when j is interstitial
when j is interstitial
where n is taken as the dependent species. Using these diffusivities Equation 14 now becomes,
Equation 18 contains the so-called interdiffusion coefficients, sometimes referred to as chemical diffusivities. These diffusivities may be evaluated experimentally from e.g. diffusion couple experiments.
Intrinsic Diffusion Coefficients
The individual or intrinsic diffusion coefficients, that are defined in the lattice-fixed frame of reference by:
can also be evaluated from diffusion couple experiments, if in addition to concentration profiles the Kirkendall velocity can be estimated from the movement of inert markers. As the interdiffusion coefficients, the intrinsic diffusion coefficients can also be calculated from the mobilities. However, this time by applying the chain rule of derivation on Equation 10 and remembering that 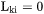 when
when 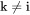 , i.e.
, i.e.
The intrinsic diffusion coefficients may be identified in Equation 20 as:
[Eq. 21]
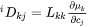
Also here there is a relation between the n concentration gradients. If one of the concentrations are chosen as dependent, and if the same approximation as previously used for the partial molar volumes of the different elements is applied, then the intrinsic diffusion coefficients defined in Equation 19 are finally found.
[Eq. 22]
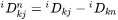 when j is substitutional
when j is substitutional
[Eq. 23]
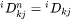 When j is interstitial
When j is interstitial
Self-diffusion Coefficient
The self-diffusion coefficient of A is the diffusivity of A in the limit of pure A. Studies of self-diffusion usually utilize radioactive tracer atoms A* of the same element.
Impurity Diffusion Coefficient
When the diffusion of a solute B in a solvent A is studied at an extremely small concentration of B, which e.g. radio tracers permit, then the impurity diffusion coefficient of B in A is observed.
References
[1992And] Andersson, Jan-Olof, and John Ågren. 1992. “Models for Numerical Treatment of Multicomponent Diffusion in Simple Phases.” Journal of Applied Physics 72 (4): 1350–55.
[1994aJon] Jönsson, Björn. 1994a. “Ferromagnetic Ordering and Diffusion of Carbon and Nitrogen in BCC Cr-Fe-Ni Alloys.” Zeitschrift Fur Metallkunde 85 (7): 498–501.
[1994bJon] Jönsson, Björn. 1994b. “Assessment of the mobility of carbon in C-Cr-Fe-Ni FCC alloys.” Zeitschrift Fur Metallkunde 85 (7): 502–9.
[1995Jon] Jönsson, Björn. 1995. “Assessment of the Mobilities of Cr, Fe and Ni in Bcc Cr-Fe-Ni Alloys.” ISIJ International 35 (11): 1415–21.
[1996Agr]Ågren, John. 1996. “Calculation of Phase Diagrams: Calphad.” Current Opinion in Solid State and Materials Science 1 (3): 355–60.
[1996Eng]Engström, Anders, and John Ågren. 1996. “Assessment of Diffusional Mobilities in Face-Centered Cubic Ni-Cr-Al Alloys.” Zeitschrift Fur Metallkunde 87 (2): 92–97.