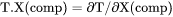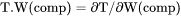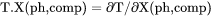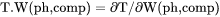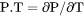Derived Variables and Partial Derivatives
Many derived variables can be obtained easily by using partial derivatives of state variables, such as heat capacity, thermal expansivity, isothermal compressibility, among others.
Derivatives of state variables can be defined or evaluated by putting a dot (.) between two state variables. The variable after the dot must be a condition that you have set when you defined your system. For example, the heat capacity (at constant pressure or volume) of a system is the partial derivative of the state variable enthalpy with respect to temperature. To evaluate this derivative, use the designation HM.T, where temperature is a state variable that you have set already.
Any partial derivative of a state variable with respect to another can be defined or evaluated as a derived variable by using the dot (.) notation.
The following table shows some examples:
| Derived Variable | Description |
|---|---|
|
|
Heat capacity for the system at either constant P if pressure is a condition or constant V if volume is a condition. |
|
|
Heat capacity for a phase at either constant P if pressure is a condition or constant V if volume is a condition. |
|
|
Heat capacity for the system multiplied by total mole number of components, i.e., |
|
|
Heat capacity for a phase multiplied by the sum of |
|
|
Thermal expansivity of the system (already multiplied by the total molar volume), i.e., |
|
|
Thermal expansivity of a phase (already multiplied by its molar volume), i.e., |
|
|
Thermal expansivity of the system (already multiplied by the total volume), i.e., |
|
|
Thermal expansivity of a phase (already multiplied by the phase volume) plus the |
|
|
Isothermal compressibility of the system (already multiplied by the total molar volume), i.e., |
|
|
Isothermal compressibility of a phase (already multiplied by its molar volume), i.e., |
|
|
Isothermal compressibility of the system (already multiplied by the total volume), i.e., |
|
|
Isothermal compressibility of a phase (already multiplied by the phase volume) plus the |
|
|
Slope of a phase boundary on a T-X(comp) phase diagram with respect to mole fraction of the component in the system. |
|
|
Slope of a phase boundary on a T-W(comp) phase diagram with respect to mass of the component in the system. |
|
|
Slope of a phase boundary on a T-X(ph,comp) phase diagram with respect to mole fraction of the component in the phase. |
|
|
Slope of a phase boundary on a T-W(ph,comp) phase diagram with respect to mole fraction of the component in the phase. |
|
|
Slope of a phase boundary on a P-T phase diagram (Note that the equilibrium with phase assemblage must be calculated first). |
Defining New Derived Variables and Functions
You can define additional derived variables or functions based on a state variable by using ENTER_SYMBOL. Any derived variable or function must have a unique name that starts with a letter and has a maximum number of eight characters. These characters can include both uppercase and lowercase letters, numerical digits and the underscore (_). No other characters are allowed.
The difference between new derived variables introduced with the ENTER_SYMBOL command and new functions introduced with the same command is as follows. Whenever Thermo‑Calc calculates the value of a function (as part of an equilibrium calculation for example), all functions related to the defined system is evaluated. An entered derived variable, on the other hand, is only evaluated when it is defined and when it is re-evaluated with EVALUATE_FUNCTIONS.
Derived Variables for Aqueous Solutions
Standard state variables used for other phases can be directly applied to the aqueous solution phase. In addition, there are pre-defined derived variables for the aqueous solution phase in particular.
Examples of predefined derived variables for the aqueous solution phase are listed and briefly described in the following tables. Some derived variables for a gaseous mixture phase are also shown. This is because EOS (Equation of State) expressions, standard thermodynamic properties and transport properties of the pure solvent H2O are also expressions and properties of the pure gaseous species H2O.
| Name | Abbrev. | Units | Description | Comments |
|---|---|---|---|---|
|
pH |
PH |
N/A |
Acidity |
of the aqueous solution phase pH = -log10(AC(H+)) = -log10(ACR(H+,AQ)) |
|
Eh |
EH |
V, mV |
Hypothetical electric potential |
of the aqueous solution phase Eh = u(ZE)/96485.309 |
|
Pe |
PE |
N/A |
Logarithm of the hypothetical electron activity |
of the aqueous solution phase pe = u(ZE)/(2.3025851*RT) |
|
Ah |
AH |
kJ, kcal |
Thermodynamic affinity per electron |
of a redox couple wrt the standard hydrogen electrode in the aqueous solution phase Ah = u(ZE) |
|
yw |
YH2O |
N/A |
Mole fraction |
of the solvent H2O in the aqueous solution phase YH2O = Y(AQ,H2O) |
|
Nw |
AH2O |
mole |
Mole number |
of 1.0 kg of solvent H2O AH2O = 55.508435 |
|
Nsp |
NSH2O |
mole |
Mole number, NS(AQ,H2O) |
of the solvent (H2O) in the aqueous solution phase NS(AQ,H2O) = YH2O*NP(AQ) |
|
NS# |
Mole number, NS(AQ,sp) |
of a solute species in the aqueous solution phase NS(AQ,sp) = Y(AQ,sp)*NP(AQ) |
||
|
M |
ML# |
mol/kg_H2O |
Molality, ML(AQ,sp) |
of a solute species in the aqueous phase ML(AQ,sp) = Y(AQ,sp)*AH2O/YH2O |
|
m* |
TIM |
equivalent molality |
Total molality |
of all solute species in the aqueous solution phase TIM = sum[ML(AQ,sp)]ions + sum[ML(AQ,sp)]complexes |
|
mt |
TIC# |
equivalent molality |
Total ionic concentration, TIC(AQ,sp) |
of a cation I in the aqueous phase TIC(AQ,spI) = sum[ML(AQ,spJ)*V(spI-in-spJ)] |
|
I |
ISTR |
N/A |
Ionic strength |
of the aqueous solution phase ISTR=1/2*sum[ML(AQ,sp)*Z(AQ,sp)**2] |
|
γ |
RCH2O |
N/A |
Activity coefficient, RC(H2O,AQ) |
of the solvent (H2O) RC(H2O,AQ) = ACR(H2O,AQ)/YH2O |
|
RC# |
Activity coefficient, RC(sp,AQ) |
of a solute species RC(sp,AQ) = ACR(sp,AQ)/Y(AQ,sp)*YH2O |
||
|
αi |
AIH2O |
N/A |
Activity, AI(H2O,AQ) |
of the solvent (H2O), AI(H2O,AQ) = ACR(H2O,AQ) |
|
AI# |
Activity, AI(sp,AQ) |
of a solute species related to the aqueous solution phase, AI(sp,AQ) = ACR(sp,AQ)*AH2O |
||
|
LogAI# |
Log10 Activity, LogAI(H2O,AQ), LogAI(sp,AQ) |
of the solvent or a solute species related to the aqueous solution phase in common logarithm, LogAI(H2O,AQ) = log10[AI(H2O,AQ)] LogAI(sp,AQ) = log10[AI(sp,AQ)] |
||
|
αw |
AW |
N/A |
Activity |
of H2O in the aqueous solution phase AW = ACR(H2O,AQ) |
|
ɸ |
OS |
N/A |
Osmotic coefficient |
of aqueous solution phase OS = -55.508435*lnAW/TIM |
|
At1 |
AT1 |
equil_mol/kg_H2O |
Titration alkalinity (definition 1) |
of the aqueous solution phase Generally defined as the equivalent molality of carbonate and bicarbonate at the methyl orange endpoint (pH=4.5). |
|
At2 |
AT2 |
equil_mol/kg_H2O |
Titration alkalinity (definition 2) |
of the aqueous solution phase Generally defined as the equivalent molality of carbonate and bicarbonate, plus sulfide, at the methyl orange endpoint (pH=4.5). |
| Name | Abbrev. | Units | Description | Comments |
|---|---|---|---|---|
| γ |
RA# |
N/A |
Activity coefficient, RA(sp,GAS) |
of a gaseous species in the gaseous mixture RA(sp,GAS) = function(Y,T,P) |
|
γ* |
RF# |
N/A |
Fugacity coefficient, RF(sp,GAS) |
of a pure gaseous species under TP RF(sp,GAS) = function(T,P/V) |
|
F |
FUG# |
pa, bar, psi |
Fugacity, FUG(sp,GAS) |
of a gaseous species in the gaseous mixture FUG(sp,GAS) = RA(sp,GAS)*RF(sp,GAS)*Y(GAS,sp)*P |
|
ft |
TFUG |
pa, bar, psi |
Total gas fugacity |
of the gaseous mixture phase TFUG = sum[FUG(sp,GAS)] |
Defining New Derived Variables for Aqueous Solutions
You can define many different additional derived variables and functions. For instance, the partition coefficient of a component between two phases is defined as follows:
Pc<name> = X(phase1,component)/X(phase2,component)
Another example is the activity coefficient of a component in the system. It is defined as follows:
Rc<name> = ACR(component)/X(component)
The activity coefficient of a species in a solution phase depends on which model definitions on the reference states that are used and it depends on the standard states for the species. If the standard state of a species is defined to be the same as the pure species in a substitutional phase, then the activity coefficient of the species can be calculated as:
RC<name> = ACR(species,phase)/Y(phase,species)
In some cases, there are more than one sublattice in the phase and the reference states for the phase species cannot be presented by the pure species, as in the case of C in FCC [(Fe)1(C,N,VA)1], where the model may end at fifty percent C and fifty percent Fe. In those cases, the chemical potential and activity of all phase constituents is not well defined and you cannot properly define the activity coefficients of the species in the phase.
For an aqueous solution phase, no matter what model is used, the reference state and standard state for both the solvent and solutes are defined in a special way in the Thermo‑Calc software. The reference state for the solvent is set as pure water, the same as its standard state (according to Raoults's Law). The standard state for a solute species is set the hypothetical solute species, whilst its reference state is defined as the hypothetical state at unit molality (one mole dissolved into 1.0 kg of solvent) but in which the environment of each molecular is the same as at infinite dilution (according to Henry's Law). Under these definitions, the activity coefficients for solvent species can be calculated as follows:
RC<H2O> = ACR(H2O,aqueous)/ Y(aqueous,H2O)
The coefficients for the solute species can be calculated as follows:
RC<spec> = AI(species,aqueous)/ML(aqueous,species)
= ACR(species,aqueous)/ Y(aqueous,species)*Y(aqueous,H2O)
AI is here the activity of solute species calculated from the model, and ML is the molality of the species.
Thermodynamic Variables and Wildcard Characters
The ACR (species,phase) and the MUR (species,phase) quantities can only be appropriately and meaningfully applied to substitutional solution phases (such as GAS, AQUEOUS, LIQUID) and to solution phases without an interstitial sublattice set. This means that the wild card characters * and $ normally don’t work properly for the activity and/or chemical potential properties.
For example, do not use ACR(*,*) or MUR(*,*) for all the species relative to all phases, nor ACR(*,phase) or MUR(*,phase) for all the species relative to a specific phase, nor ACR(species,*) or MUR(species,*) for a specific species relative to all phases.
Instead, use specific names for species and (applicable) phase, as in the following examples:
SHOW_VALUE acr(fe+2,aqueous)Lists activity of the Fe+2 species referred to AQUEOUS solution phase
SHOW_VALUE mur(c2,gas)Lists chemical potential of the C2 species referred to GAS mixture phase
SET_AXIS_VAR y ac(o2,gas)Sets activity of the O2 species referred to GAS mixture phase as Y-axis
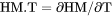
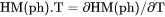
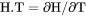
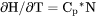 if pressure is a condition in a closed system or
if pressure is a condition in a closed system or 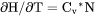 if volume is a condition in a closed system.
if volume is a condition in a closed system.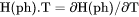
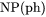 and
and 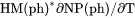 , i.e.,
, i.e., 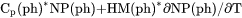 if pressure is a condition or
if pressure is a condition or 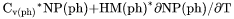 if volume is a condition.
if volume is a condition.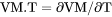
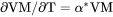 .
. 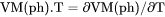
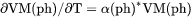 .
.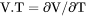
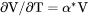 .
.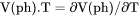
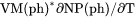 term, i.e.,
term, i.e.,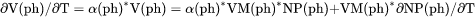 .
.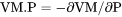
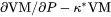 .
.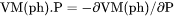
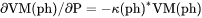 .
.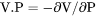
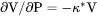
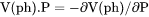
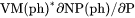 term, i.e.,
term, i.e.,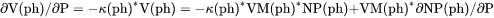 .
.