Setting Up the Multiphase Simulation
Set the temperature T during the simulation to 1100° C (1373.15 K) and enter a region diffcouple.
go dictra-monitor
set-cond glob T 0 1373.15; * N
ent-reg diffcouple
ent-grid
diffcouple
3e-3
auto
set-auto-grid-option
fine
The automatic (auto) grid point distribution is used as with the other examples. One more command SET-AUTO-GRID-OPTION is used and fine is chosen to set the number of equidistant points in a region (e.g. maximum distance between two adjacent grid points is the size of the region divided by this number) and the maximum factor that is allowed in the geometric series defining the initial grid.
As always, a region must contain exactly one active phase that is of type matrix. In this example it is arbitrary whether it is the bcc or the fcc phase that is entered as matrix.
enter-phase
active
diffcouple
matrix
fcc
The bcc phase is entered in the same manner as the fcc phase, except that the type is set as spheroid.
enter-phase
active
diffcouple
spheroid
bcc
The initial composition profile of the fcc phase is entered as a function of distance.
enter-composition
diffcouple
fcc
fe
m-f
cr
function
2.57e-1+(4.23e-1-2.57e-1)*hs(x-1.5e-3);
ni
function
6.47e-2+(2.75e-1-6.47e-2)*hs(x-1.5e-3);
In the above entries, the hs denotes the Heaviside step function that has the following properties:
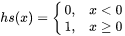
The resulting Cr profile is thus 0.257 on the left half of the domain and 0.423 on the right with a sharp step at the center.
As shown in About the Multiphase Simulation.
The initial composition of the fcc phase is actually the initial overall composition. This is due to the choice of initial composition of the spheroid bcc phase.
ENTER_COMPOSITIONS
<REGION NAME>
<PHASE NAME>
<USE EQUILIBRIUM VALUE Y/N>
enter-comp
diffcouple
bcc
y
When entering the composition for a type spheroid phase it is possible to either, as here, let the composition of the matrix phase be the overall composition or manually enter a start composition and volume fraction.
The local kinetics of the multiphase mixture must be estimated by means of some function that may depend on the local phase fractions, phase compositions and the mobilities of the individual phases. The command for choosing the function to use is ENTER_HOMOGENIZATION_FUNCTION. There are many such homogenization functions to choose from. In this particular example the so-called lower Hashin–Shtrikman bound [1962Has] is a good choice.
ENTER_HOMOGENIZATION_FUNCTION
<ENTER FUNCTION NUMBER>
enter-homo-fun
1
Finally, set simulation time (100 h) and select the name of the result file:
set-sim-time
3.6e5
yes
3.6e4
1e-7
1e-7
save multiphase_example y
Reference
[1962Has] Z. Hashin, S. Shtrikman, A Variational Approach to the Theory of the Effective Magnetic Permeability of Multiphase Materials. J. Appl. Phys. 33, 3125–3131 (1962).