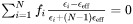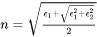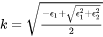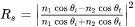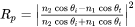About the Optical Properties - Noble Metals Property Model

The Optical Properties - Noble Property Model, available with the Property Model Calculator and the Noble Metal Alloys Model Library, is used to simulate the color, reflection, and transmission of light, based on modeling the alloy microstructure and the resulting optical properties. This model is currently applicable for the Au-Al-Ag-Cu-Pt system.

For an example see PM_Noble_01: Color Prediction.

In the text CIE is the abbreviation for Commission internationale de l'éclairage (International Commission on Illumination), which is the international authority on light, illumination, color, and color spaces.

To run calculations with the Noble Metal Alloys Models (as part of the Noble Metal Alloys Model Library) requires a valid maintenance license plus a license for the TCNOBL (version 3 and newer) database.

The input parameters are entered on the Configuration window for the Property Model Calculator. There are also settings on the Plot Renderer where you can choose from the available and relevant axis variables.

See Optical Properties - Noble Metals Property Model Settings

Background

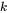The Optical Properties - Noble model simulates the color and optical properties such as refractive index and extinction coefficient for a given condition. The process to simulate those properties has four steps.

The first step is to calculate the composition and phase fractions for phases using the Equilibrium Calculator. Once that is done, you calculate the dielectric function 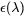of an alloy: 

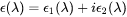
where 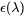is the complex dielectric function of wavelength, 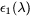is the real part of the dielectric function, representing the material’s ability to polarize in response to an electric field, thus affecting refraction, and is the imaginary part of the dielectric function, representing the energy loss or absorption in the material.

Thermo-Calc calculates the dielectric functions of FCC_A1 and L12_FCC phases with different Al, Au, Ag, Cu, and Pt content. The TCS Noble Metal Alloys Database (TCNOBL) calculates dielectric functions that cover intermetallic phases AL2CU_C16, AL3NI2 (PT)_D513, ALPT_B20, CUPT_L11, AL2AU_C1_CAF2, PTAL2, and CU9AL4. For alloys containing multiple phases, the Bruggeman model [2001Mar] is adopted to get the effective dielectric functions based on the phase fraction and dielectric functions of each individual phase. For N different phases, the generalized Bruggeman model equation is:

[Eq. 1]         

Where:

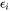• is the dielectric function of the i-th phase.
• is the volume fraction of the i-th phase, and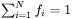
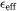• is the effective dielectric constant of the composite material.

The third step is obtaining refractive index and 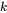from dielectric functions using Eq. 2 and Eq. 3.

[Eq. 2]         

[Eq. 3]         

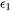and 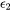are the real and imaginary parts of dielectric functions, respectively.

The fourth step is to calculate reflectivity of the material using Fresnel equations (Eq. 4 and Eq. 5) [2023Gri], which describes how much light is reflected and transmitted when it strikes from material 1 to the surface of material 2 at a specific angle. For light striking the surface at an oblique angle 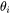, the Fresnel equations differ for s-polarized and p-polarized light. For more complex situations such as thin films and multiple materials layers, the transfer matrix method (TMM) is used [2016Byr]:

[Eq. 4]         

[Eq. 5]         

Where:

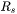• : The reflectance for s-polarized light.
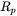• : The reflectance for p-polarized light.
• : The complex refractive index of material 1 (include real and imaginary part). In the current version material 1 is set to be air.
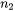• : The complex refractive index of material 2 (include real and imaginary part).
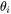• : The angle of incidence (angle between the incident light and the normal to the surface).
• : The transmission angle (or angle of refraction), calculated using Snell’s law: .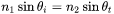

The last step is to calculate the color coordinates by using the CIE XYZ color space and integrating over the visible spectrum [2019Pra]:

[Eq. 6]         

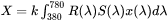
[Eq. 7]         

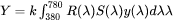
[Eq. 8]         

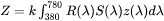
Where:

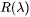• is the reflectance of the material as a function of wavelength 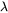, where it is calculated using the calculated materials and 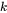and Fresnel equations.
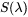• is the spectral power distribution of the illuminant (for example, the CIE D65 illuminant represents average daylight).
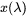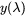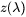• , , and are the CIE color-matching functions that model the human eye’s response to different wavelengths of light.
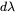• is the differential element over the visible spectrum (400 nm to 700 nm).
• is a normalization constant chosen so that Y = 100 for a perfectly reflective material.

Finally, the tristimulus values for the color of the material is found and based on its reflectance spectrum.

You can further convert these tristimulus values into other color spaces, such as CIE LAB or sRGB, depending on the display or application requirements. See About Color Space.

About DeltaE (ΔE)

Delta E (ΔE, dE) is a metric to understand how the human eye perceives color difference. On a typical scale, the ΔE value ranges from 0 to 100. The larger the ΔE value, the more perceptible the color difference.

If ΔE is:

• Smaller than 2 (ΔE < 2), it is hard to find the color difference.
• In the range of 2 – 10, you can find the difference at a glance.
• Between 11 and 49, colors are more similar than opposite.
• Between 50 to 99, colors are more opposite than similar.
• 100, colors are the exact opposite.

This is a general guideline and it is possible to get a ΔE value below 1.0 for two colors that appear different. This is the case with CIE 1976 and CIE 1994 formulas, in which saturation is either not considered or not weighted properly. For the Optical Properties Model there are three methods for calculating ΔE. Because of inconsistencies between the three algorithms, the exact meaning of ΔE changes slightly depending on which formula is used.

ΔE Method

When you select the Calculate ΔE value checkbox, an additional setting, ΔE method is available. This section describes the options CIE 1976, CIE 1994, and CIE 2000 (default).

Over time, several versions of ΔE have been developed to improve how accurately they represent human color perception. The most common versions are ΔE 1976, ΔE 1994, and ΔE 2000. Each one has improvements in accuracy for different use cases.

• ΔE 1976 formula (CIE 1976) was the first standardized method to calculate color differences and is based on the CIE 1976 Lab color space. It uses the Euclidean distance between two colors in this three-dimensional space. It is simple and easy to compute, however it has limitations. For example, it treats all changes in color as being equally perceptible, even though the human eye is more sensitive to changes in lightness and less sensitive to changes in chroma (color saturation).
• ΔE 1994 CIE 1994 was introduced to address the limitations of ΔE 1976 by considering the non-uniformity of human color perception. It adjusts for differences in lightness, chroma, and hue. It is widely used in industrial applications such as textiles, coatings, and plastics but it still does not perfectly match human visual perception.
• ΔE 2000 CIE 2000 is the most recent and accurate method to calculate color differences. It is designed to improve on ΔE 1994 and provides a more perceptually uniform color difference metric, considering additional corrections for viewing conditions and color perception anomalies. It is the best choice for applications where precise color matching is crucial.

About the Standard Illuminant

There are several options to choose from in the Standard illuminant list. These options are related to how the color of alloys is simulated under different lighting conditions. Each option represents a specific type of light source with a defined spectral power distribution (SPD), which describes the intensity of light at different wavelengths. The choice of illuminant affects the perceived color of an object.

The following is an overview of the most common standard illuminants available to select.

• Single wavelength: Choose this when you want to know and 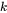value at certain wavelengths. When selected, color is not calculated.
• A: Illuminant A represents typical tungsten incandescent lighting, with a color temperature ~2856 K. Use case: Indoor lighting conditions.
• B: Illuminant B represents noon sunlight, with a color temperature ~4874 K. Use case: Daylight conditions with direct sunlight. Often replaced by D series illuminants.
• C: Illuminant C represents average daylight, with a color temperature ~6774 K. Use case: Color matching in daylight, superseded by the D-series illuminants.
• Illuminant D Series represents different types of daylight with varying color temperatures
  • D50: ~5003 K, warm daylight at sunrise or sunset.
  • D55: ~5503 K, mid-morning or mid-afternoon daylight.
  • D65: ~6504 K, the most common standard for noon daylight conditions. This is the default for the Property Model.
  • D75: ~7500 K, used for north sky daylight, that has been largely replaced by D65.
• E: Illuminant E is theoretical, equal-energy illuminant, with no color temperature as it is theoretical. Use case: Represents uniform energy across all visible wavelengths, often used in colorimetric calculations as a reference.
• Illuminant F Series illuminants represent various types of fluorescent lighting, commonly found in offices, retail environments, and other indoor spaces. The number after "FL" corresponds to different types of fluorescent bulbs.
  • FL1: 6430, daylight fluorescent.
  • FL2: 4230, cool white fluorescent.
  • FL3: 3450, white fluorescent.
  • FL4: 2940, warm white fluorescent.
  • FL5: 6350, daylight fluorescent.
  • FL6: 4150, light white fluorescent.
  • FL7: 6500, D65 simulator, daylight simulator.
  • FL8: 5000, D50 simulator, Sylvania F40 Design 50.
  • FL9: 4150, cool white deluxe fluorescent.
  • FL10: 5000, Philips TL85, Ultralume 50.
  • FL11: 4000, Philips TL84, Ultralume 40.
• LED Illuminants represent different LED lighting sources, which are becoming more common as replacements for traditional incandescent and fluorescent lighting. They often focus on different spectral distributions.
  • LED-B1 to LED-B5: Represents different types of blue-enhanced LED lights.
  • LED-BH1 defines a blend of phosphor-converted blue and a red LE.
  • LED-V1 and LED-V2: Represents different types of violet-enhanced LED lights
  • LED-RGB1: Represents RGB LED lights, where colors are mixed from red, green, and blue LEDs.

In summary:

• D65 is typically used to simulate daylight when designing digital displays or performing color matching in industrial settings.
• Illuminant A is used to simulate indoor lighting conditions with tungsten bulbs.
• Fluorescent (FL series) and LED illuminants are used when you need to simulate environments using these artificial light sources.

About the Viewing Angle

The Viewing angle options are CIE 1931 2 Degree Standard Observer or CIE 1964 10 Degree Standard Observer.

The CIE 2° and CIE 10° Standard Observers are models that describe how an average human eye perceives color. They are based on experiments that measured human color vision using color matching functions. These functions describe how different wavelengths of light are combined by the human eye to match a perceived color. The main difference between the two observers lies in the angle of view they represent, which corresponds to different parts of the eye's visual field.

• CIE 1931 2° Standard Observer model is based on experiments where subjects matched colors within a 2° field of view. This small angle represents the central vision, which is the part of the eye responsible for seeing fine detail. It is most accurate to view small objects or when details are seen up close, such as tiny pixels on a screen or small color samples.
• CIE 1964 10° Standard Observer model represents color perception over a 10° field of view, a much larger area than the 2° observer. This wider field involves more of the peripheral vision, provides a broader and more comprehensive representation of how the eye perceives color in general viewing situations. This is better for measuring color in typical situations where larger objects are viewed, such as printed materials, paints, textiles, or any larger surface.

About Color Space

A color space organizes colors to ensure consistent representation across devices. The Color space options are used in two sets of settings and in both you have the option to choose LAB (default), sRGB, or XYZ.

• CIE LAB (the default) includes all visible colors and is ideal for color matching, quality control, and any application where accurate perceptual color differences matter.
• CIE XYZ covers all perceivable colors and is best for scientific and colorimetric studies, where precise color representation and transformations are needed.
• sRGB has a smaller color gamut, but it is widely used for displaying on consumer electronics

CIE LAB Color Space (CIE LAB)

CIE LAB was introduced by the CIE in 1976, and was designed to overcome some of the limitations of CIE XYZ. It created a color space that is perceptually uniform, meaning that a given change in color value should correspond to a similar level of perceived difference to the human eye.

CIE XYZ Color Space

Developed in 1931 by the CIE, which was based on tristimulus values—X, Y, and Z—that are hypothetical primaries derived from human vision experiments. It aims to represent all visible colors using a mathematical model grounded in human color perception.

sRGB Color Space

sRGB (Standard Red Green Blue) was created by HP and Microsoft in 1996 as a standard color space for digital displays and the internet webpage. It is based on the typical capabilities of a standard CRT monitor and has become the default color space for web images, digital photography, and many consumer-level devices like cameras and printers.

References

[2001Mar] A. Marini, G. Onida, R. Del Sole, Quasiparticle Electronic Structure of Copper in the GW Approximation. Phys. Rev. Lett. 88, 016403 (2001).

[2016Byr] S. J. Byrnes, “Multilayer optical calculations” (2016); http://arxiv.org/abs/1603.02720.

[2019Pra] G. Prandini, G.-M. Rignanese, N. Marzari, Photorealistic modelling of metals from first principles. npj Comput. Mater. 5, 129 (2019).

[2023Gri] D. J. Griffiths, Introduction to Electrodynamics (5th Edition) (Cambridge University Press, 2023).