Solution Models in the GIBBS (GES) Module
The AMEND_PHASE_DESCRIPTION command is used to specify/amend phase descriptions if a phase has a miscibility gap, uses a special excess energy model, or has a specific additional contribution to its Gibbs energy, for example.
This topic outlines the application of each option and includes important information about each command.
There are many solution models implemented in the GIBBS module (type INFO MODELS to see details about various thermodynamic models). However, these are switched on and handled differently via various GIBBS routines/commands:
- The first models the non-ideality as excess parts, i.e. by amending the phase’s EXCESS_MODEL and/or TERNARY_EXTRAPOLAT models.
- The second models the non-ideality as ADDITIONAL parts, i.e. by amending the phase’s other subjects in this command, e.g. MAGNETIC_ORDERING for the Magnetic Ordering Model, DISORDERED_PART for the CVM Approach in modeling chemical ordering/disordering phenomenon, QUASICHEM_IONIC for using a quasi-chemical entropy term for an ionic two-sublattice liquid solution phase, QUASICHEM_FACT00 or QUASICHEM_IRSID for describing a substitutional liquid solution phase, DEBYE_HUCKEL for the DHLL/SIT Model in describing a dilute aqueous solution phase, etc.
- The third implements the model entirely or partially into the GIBBS module and related database(s), such as for the electrostatic contribution in an AQUEOUS solution phase by the Complete Revised_HKF Model, the Murngham Model, Birch-Murngham Model or Generalized PVT Model for high-pressure/temperature volume contribution in a solid or liquid phase, the SUPERFLUID Model for the non-ideal EOS and non-ideal mixing in a gaseous mixture.
Use this if you want to add a new constituent to a phase. It is illegal to add new constituents to an ionic two-sublattice liquid phase.
Use this to change the names of some specific phases. For example, a phase called FE3O4_S may be better named Magnetite to help identify it during the calculations and postprocessing. This is also a way to delete a phase by hiding it under a new name.
Use this to change the number of sites (i.e. the stoichiometric coefficients of various sublattices) in a sublattice phase.
Use this for solution phases that may have miscibility gap(s). However, this is less important today and often unnecessary to define additional composition set(s), since the implemented Global Minimization Technique can usually detect and add such composition set(s) in an automatic manner where it is really necessary during equilibrium calculations (of single-points, stepping or mapping).
Use this to set major constituent(s) on each sublattice in each composition set for a solution phase. This is useful to make calculations converge faster because it may simplify giving start values when calculating the equilibrium as those phases with miscibility gaps should have different major constituents for each composition set. The databases often set major constituents for several phases automatically when data are retrieved.
Use this to limit the application range (in terms of mole-fractions of all the involved elements) of a particular solution phase. This is useful to avoid automatic creations (enforced by the Global Minimization Technique) of additional composition sets for some solution phases (such as AQUEOUS solutions or dilute Fe-based liquid mixtures) of which the used models [e.g. the SIT Model or the Complete Revised_HKF Model for AQUEOUS solution, or the modified dilute solution parameters (plus a quadratic term, according to Hillert (1986) based on the SigworthElliot Model [1974Sig] for Fe-rich liquid mixture] cannot be appropriately applied on a full scale.
Globally set the composition limits (in terms of mole fractions of various elements) in a specific solution phase, so that whenever the program finds a potential phase composition or a new composition set of possible miscibility gap(s) but that is out of this globally-set composition range, the program automatically ignores such a phase composition in an equilibrium calculation. This can be done either permanently inside a database (by enforcing this option for amending the phase-description of the solution phase) or temporarily within the GIBBS module (by using this phase-description amendment option).
This is important for solution phases for which the thermodynamic models and assessed data for the phases are for specific composition ranges, for example, the FE_LIQUID phase in the SLAG database is only applicable for Fe-rich liquid mixture, and the AQUEOUS phase in the TCAQ/PAQ and AQS/PAQS databases is only applicable for H2O-dominant aqueous solution phase.
Specify the low and high mole-fraction limits for each of the elements possibly available within the considered phase (in the currently defined system, or in a certain database). Do this for all the possible elements (defined in the phase) in a single AMEND_PHASE_DESCRIPTION FRACTION_LIMITS command-sequence, for example:
TYPE_DEFINITION R GES AM_PH_DES FE_LIQUID FRACTION_LIMITS Fe 0 0.6
Ag 0 0.01 Al 0 0.05 Ca 0 0.05 Co 0 0.01 Cr 0 0.01
Cu 0 0.02 Mg 0 0.05 Mn 0 0.05 Mo 0 0.05 Nb 0 0.05
Ni 0 0.05 Pb 0 0.05 Si 0 0.10 Sn 0 0.02 Ti 0 0.05
U 0 0.01 V 0 0.02 W 0 0.02 Zr 0 0.03
B 0 0.01 C 0 0.01 H 0 0.01 N 0 0.01 O 0 0.01
P 0 0.01 S 0 0.01 !
The contribution from the disordered phase are added to the ordered phase. Use this to avoid entering several parameters to the ordered phase in the database. Instead it can be expressed as one parameter in the disordered phase.
The reference [2018Sun] section 2.3.4 has extensive details about this model. Original references from [1994Dup] and [2000Ans].
This command is needed for the special treatment of chemically-ordered phases where the contributions from the disordered state are described by a phase without ordering sublattices (the disordered phase name must be specified).
Several checks are made that the ordered and disordered phases are compatible (sublattices, sites and constituents). A link is then created between the phases, and the disordered phase is hidden from application programs. The Gibbs energy for the ordered phase also includes the Gibbs energy for the disordered phase.
Phases which can have an order/disorder transformation have parameters split on two phases and are referred to as the two phase description in the GIBBS module. One of them has sublattices for chemical ordering, the other one represents the disordered state. Normally, the ordered BCC and FCC or HCP phases may have either 2 or 4 substitutional sublattice (plus one additional interstitial site), that are handled by the Two Substitutional-Sublattice Ordering Model or Four Substitutional-Sublattice Ordering Model, respectively.
Two phase means that the ordered phase has parameters that describe the ordering. The disordered phase has all parameters for the reference state and those for describing the disordered phase. The ordered phase may occur only is some systems whereas the disordered phase may occur frequently, typical examples are the disordered FCC and BCC which may become ordered as L12 or B2 in certain systems. In order to treat multicomponent systems where some subsystems have ordering it would be necessary to transform all parameters of BCC into a B2 model.
The parameters describing the disordered phase are not changed but the Gibbs Energy system is informed that the Gibbs Energy for the two phases should be added.
The method used calculates the Gibbs Energy of a two phase model with two or four substitutional sublattices for ordering.
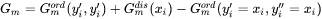
The mole fractions xi are calculated from the site fractions yi. The last term means that the contribution from Gmord in a disordered state (same site fraction, equal to the mole fraction, on both sublattices) is subtracted. The effect of this is that the parameters in the ordered phase have no contribution to the disordered state.
Change the magnetic ordering parameter for a certain phase with magnetic ordering contribution, in terms of its anti-ferromagnetic factor. By default this is –1 for BCC phase and –3 for all other phases (FCC, HCP, etc.). The fraction value of the total enthalpy (due to short-range ordering above the magnetic transition temperature) is by default 0.40 for BCC phase and 0.28 for all other phases (FCC, HCP, etc.).
See example tcex52.
Use this to change the default Excess Model (for interaction energies) from the default (REDLICH-KISTER_MUGGIANU). The model handles the excess interaction energies in a solution phase is chosen from:
- REDLICH-KISTER_MUGGIANU: for binary (R-K) & ternary (R-K-M) interactions
- REDLICH-KISTER_KOHLER: for binary (R-K) & ternary (R-K-K) interactions
- FLORY-HUGGINS POLYMER MODEL: for interactions in a polymer mixture phase (F-H)
- MIXED-EXCESS-MODELS: (R-K default) for mixed binary excess model (R-K, Legendre & Polynom) of a substitutional solution phase
- HKF: for interaction in an AQUEOUS solution phase (HKF)
- PITZER: for interaction in an AQUEOUS solution phase (PIT)
- CENTRAL_ATOM_MODEL: for interaction in a liquid slag solution phase (C-A-M)
For extrapolations of excess energies from related binary systems to ternary or higher-order systems, the Redlich-Kister binary excess interaction parameters may be extrapolated with either a Muggianu extension (i.e. the default REDLICH-KISTER_MUGGIANU model) and a Kohler extension (i.e. the alternative REDLICH-KISTER_KOHLER model), where there is no ternary, quaternary or higher-order interaction parameter.
The REDLICHKISTER_KOHLER model is implemented only for ternary systems.
The MIXED-EXCESS-MODELS option works only for a substitutional phase with no sublattice (such as the metallic LIQUID phase) and it can be used to invoke asymmetrical simple or Legendre polynomial as binary excess energy models in addition to the default symmetrical Redlich-Kister model for the chosen pair of constituents in a substitutional phase with no sublattice. Asymmetrical here means that the power series depend only on one of the constituents, for example with expansions based on the [1-2*X(B)] term rather than [X(A)X(B)].
Binary interaction parameters for such a pair of constituents must be entered prior to turning on the non-default Legendre or Polynom models.
See example tcex52.
Use this to change the extrapolation method from the default REDLICH-KISTER_MUGGIANU to another extrapolation model. This method extrapolates from binary to ternary (and higher-order) excess interaction parameters in a solution phase and is chosen from:
- MUGGIANU for Muggianu Extrapolation from R-K parameters
- TOOP-KOHLER for Toop-Kohler Extrapolation Model
- KOHLER-ALL for Kohler Extrapolation Model
- MUGGIANU_RESTOR for Muggianu-Restor Extrapolation Model
Only when all the relevant binary excess energies in the current solution phase are treated by the default Redlich-Kister Model (i.e. the Mixed-Excess-Model should have not been used), the MUGGIANU_RESTOR method for ternary extrapolations is equivalent to the Redlich-Kister_Muggianu Model, or the KOHLER-ALL method to the RedlichKister_Kohler Model.
The default ternary extrapolation method MUGGIANU_RESTOR applies to a solution phase as a whole, whatever the binary excess model(s) enforced to each of individual binary pairs in the phase. In case that all the binary pairs in the phase use the default binary excess model REDLICH-KISTER, then the ternary extrapolation method becomes the so-called Redlich-Kister_Muggianu Model (in short as R-K-M), for extrapolations from binary parameters to ternary (and higher-order) excess energy terms; when no ternary L parameter is entered for that, such a default R-K-M Model is always used.
The KOHLER-ALL ternary extrapolation method can be turned on also for a solution phase as a whole, whatever the binary excess model(s) enforced to each of individual binary pairs in the phase. In case that all the binary pairs in the phase use the default binary excess model.
REDLICH-KISTER, then the ternary extrapolation method becomes the so-called Redlich-Kister_Kohler Model (in short as R-K-K), for extrapolations from binary parameters to ternary (and higher-order) excess energy terms; when no ternary L parameter is entered for that, such an R-K-K Model is used.
The TOOP-KOHLER ternary extrapolation method is applied in a special way: for a specific ternary system (e.g. A-B-C) in a solution phase, specify which two constituents as the so-called Kohler constituents and the remaining constituent as the so-called Toop constituent on a given sublattice. If for the A-B-C ternary system you have specified A and B, or B and A, as the Kohler constituents (entered as the basis constituent and first interacting constituent) and C as the Toop constituent, only the A-B binary interaction parameters are used in accordance with the Kohler ternary extrapolation formula for A-B-C ternary interaction, while any other binary interaction parameters involving the Toop species C (i.e. of A-C and B-C binaries) are used in line with the Toop-Kohler ternary extrapolation formula (for the A-C-B and B-C-A ternary interactions).
To use the DHLL (Debye-Hückel Limiting Law) model and SIT (Specific Ionic Interaction Theory) model for a dilute AQUEOUS solution phase, switch the DEBYE_HUCKEL part on, and it removes previously set (if any) ADDITIONAL part on the non-ideality for the chosen AQUEOUS phase.
To use the hypothetical electrostatic contribution for the chosen phase (it must be an aqueous solution phase using the Complete Revised_HKF Model). It removes previously set (if any) ADDITIONAL part on the non-ideality for the chosen AQUEOUS solution phase.
To use the Quasichemical-Ionic model for the chosen liquid phase, you must have already entered/retrieved a liquid phase as an ionic two-sublattice liquid solution phase (normally, that is the IONIC_LIQ phase), and then use this amending option to switch QUASICHEM_IONIC on. It creates a completely new liquid solution phase [namely the QUAS_IONIC phase which uses the Quasichemical Model for the entropy, according to Mats Hillert [2001Hil], while the original IONIC_LIQ phase remains in the system and is not changed by this option.
See example tcex49.
To use the Quasichemical Model developed by Kongoli et al. [1998Kon], you must have entered/retrieved a liquid phase using a normal substitutional liquid model with specified associates or species (on a single lattice site), and then turn on the option QUASICHEM_FACT00. This removes the previously-set (if any) ADDITIONAL part on the non-ideality for the chosen liquid phase.
To use the Kapoor-Frohberg-Gaye Quasichemical Cell Model (i.e. the Quasichemical Model developed by ISRID, France) for a liquid SLAG solution phase, you can use a normal liquid model with specified associates or species.
To use the special model for glass transition of a liquid phase. It removes previously set (if any) ADDITIONAL part on the non-ideality for the chosen liquid phase.
To remove all the selected ADDITIONAL part from the Gibbs energy description for the chosen phase. If preferred, set a specific phase-status bit for a phase, use the PHASE_BITS option as long you know the restrict meaning of each part of a phase- status bits.
Set phases as default-stable, which helps you to have a better guess of which phases that should be stable at the first calculation.
[1974Sig] G. K. Sigworth, J. F. Elliott, The Thermodynamics of Liquid Dilute Iron Alloys. Met. Sci. 8, 298–310 (1974).
[1994Dup] N. Dupin, Personal Communication. (1994).
[1998Kon] F. Kongoli, A. D. Pelton, Y. Dessureault, Thermodynamic modeling of liquid Fe-Ni-Cu-Co-S mattes. Metall. Mater. Trans. B. 29, 591–601 (1998).
[2018Sun] B. Sundman, Q. Chen, and Y. Du, “A Review of Calphad Modeling of Ordered Phases,” J. Phase Equilibria Diffus., vol. 39, no. 5, pp. 678–693, Oct. 2018.
[2000Ans] I. Ansara et al., “Models for composition dependence,” Calphad, vol. 24, no. 1, pp. 19–40, Mar. 2000.
[2001Hil] M. Hillert, The compound energy formalism (1). J. Alloys Compd. 320, 161–176 (2001).