Flow Stress

The Martensitic Steel Strength Property Model includes flow stress and is able to predict stress at arbitrary strain with these properties:

• True stress
• True strain (this requires user input)
• Engineering strain
• Engineering stress

The Model has a Flow stress mode to predict engineering properties such as:

• Yield strength
• Yield strain
• Ultimate tensile strength
• Uniform elongation
• Fracture strength
• Elongation at fracture
• Young’s modulus

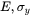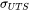True strain is not available as an input parameter when using the engineering properties mode (i.e. and , which is selected as a Flow stress mode).

Additional Information

This section is specifically about the flow stress theory and is a continuation from the main theory described in About the Martensitic Steel Strength Property Model.

The input parameters are entered on the Configuration window for the Property Model Calculator. There are also settings on the Plot Renderer where you can choose from the available and relevant axis variables.

For details about the various settings mentioned in this theory section, see Flow Stress Settings.

You can also open an installed example to see the application of these features. See PM_Fe_12: Flow Stress 15-5PH Steel for more information.

Main Implementation

The flow stress model relies on the Ramberg-Osgood equation to predict flow stress, which can be expressed as:

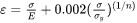
where

• is the strain,
• is the stress,
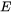• is the Young’s modulus,
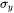• is the yield strength, and
• is the strain hardening exponent.

To calculate stress at an arbitrary strain, the parameters , , and need to be determined.

The Young’s modulus of the material is obtained by averaging the Young’s moduli of individual phases.

Elastic properties (the elastic constants and moduli) are available with the TCS Steel and Fe-alloys Database (TCFE) starting with version 14 (TCFE14). If you are using an earlier version of the database, i.e., no elastic properties are available, then the Young’s moduli of individual phases are estimated using simple rules.

The yield strength ( 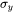) is determined based on its relationship with hardness, where the work by Pavlina and Van Tyne [2008Pav] is extended to consider a larger dataset. The hardness itself is predicted by the model as described in the primary theory section, About the Martensitic Steel Strength Property Model.

User-defined Flow Stress Parameters

Young's modulus ( 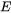) and the strain hardening exponent ( ) can be set manually by selecting the User-defined flow stress parameters checkbox on the Configuration window. The yield strength, 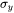, is then inferred from these parameters and the known hardness.

After selecting the checkbox, you can further choose to use the Voce equation (select this option from the Flow stress model list), which is expressed as:

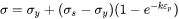
where

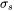• is the saturation stress,
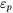• is the plastic strain, and
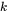• is the hardening rate.

As the Voce equation is only expressed in terms of plastic strain, the model uses 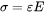for strains lower than the yield strain. To use the Voce model, you must specify the following additional settings:

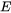• (Young's modulus)
• (Saturation stress)
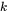• (Hardening rate)

Pre-deformed Materials

The flow stress model can be used to predict flow stress in pre-deformed materials, using the parameter Pre-straining [%]. The value given should correspond to the plastic strain that the material is exposed to beforehand. Pre-straining shifts the yield point and affects the yield strain, where uniform elongation and total elongation is then reduced by a corresponding amount.

Strain-rate Dependence

Strain-rate dependence on stress is implemented in the model and expressed as:

where

• ̇ is the applied strain rate,
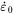• is the reference strain rate (corresponding to quasi-static conditions), and
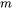• is the strain rate sensitivity, where can be predicted by the model or user-defined.

Fracture Properties

Elongation and Fracture

Neither the Ramberg-Osgood nor Voce models can be used to predict fracture properties as they are only valid for uniform deformation. In fact, modeling, e.g., total elongation in a general manner based on some physical or empirical model is a challenging task. For this reason, the total elongation is modeled using a machine learning approach. Together with other properties, total elongation can then be used to estimate the fracture strength. In the stress vs. strain mode, any engineering stress at engineering strains beyond the predicted elongation is set to NaN, signifying that the material has fractured completely.

Post-uniform True vs. Engineering Stress and Strain

The conversion between engineering and true quantities is mathematically valid in the entire range of strain, however, the conversion assumes constant volume. This assumption is not valid in the necking regime as the deformation is not distributed evenly. Furthermore, void formation would decrease the density and cross-sectional area of the specimen. These issues are not easily corrected for as they require detailed knowledge on the geometry of the necking region as a function of strain and the progression of void formation etc. Therefore, the post-uniform elongation and total elongation are only available as engineering quantities.

Gauge Length

Total elongation is the sum of uniform elongation and elongation in the necking regime, where deformation is highly localized. Therefore, post-uniform elongation scales with cross-sectional area rather than length of the test piece. Since total elongation is expressed as a percentage of the length of the test piece, the measured value of the elongation in the necking regime is dependent on the actual length of the test-piece (so-called gauge length), and thus the same is valid for total elongation. This is an artifact of improper normalization and not a material dependence. The elongation model is trained on data mostly from tests performed on samples with 50 or 80 mm gauge lengths. For martensitic steels, the difference in total elongation between these gauge lengths would not, in most cases, exceed the experimental scatter.

Reference

[2008Pav] E. J. Pavlina, C. J. Van Tyne, Correlation of Yield Strength and Tensile Strength with Hardness for Steels. J. Mater. Eng. Perform. 17, 888–893 (2008).