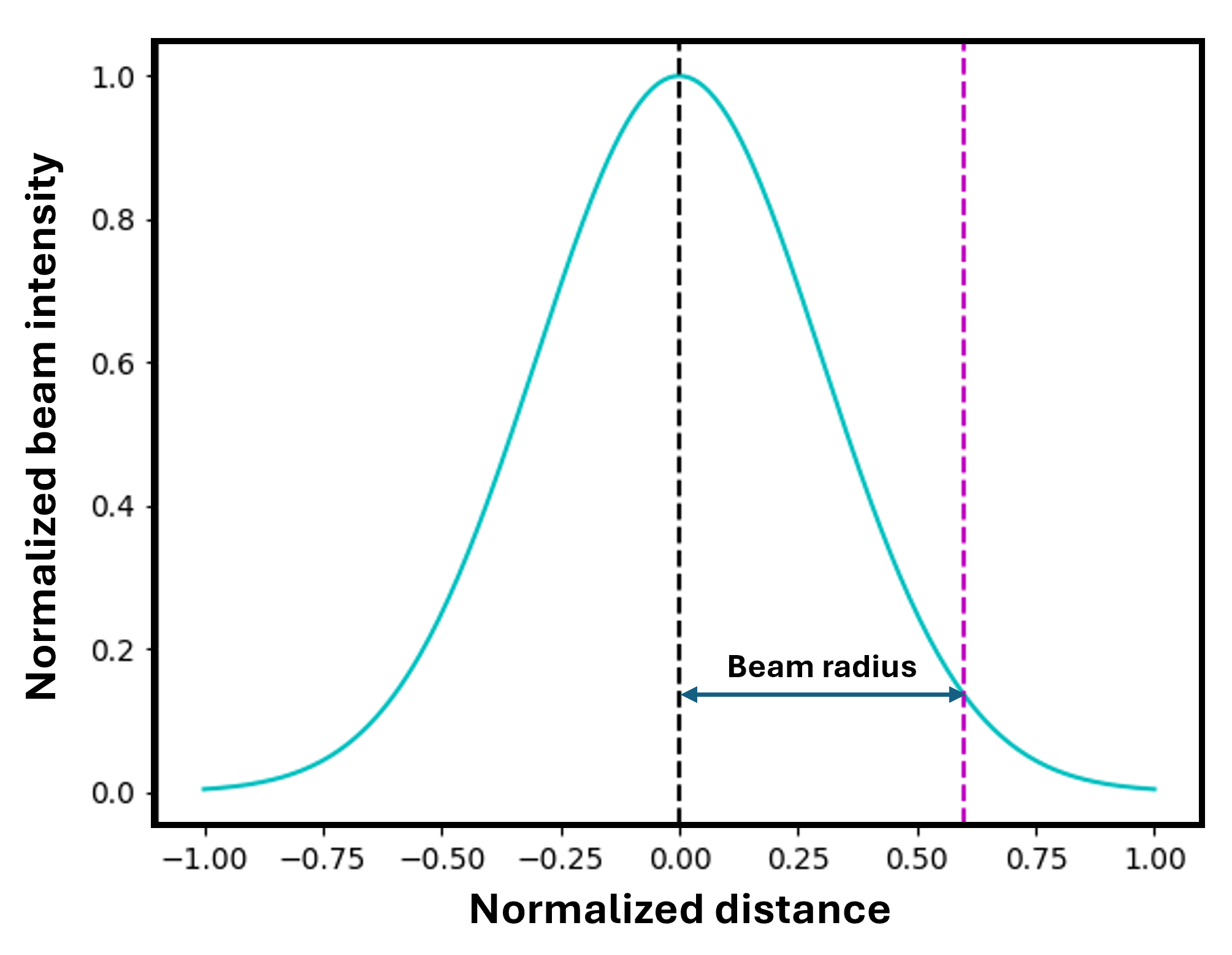
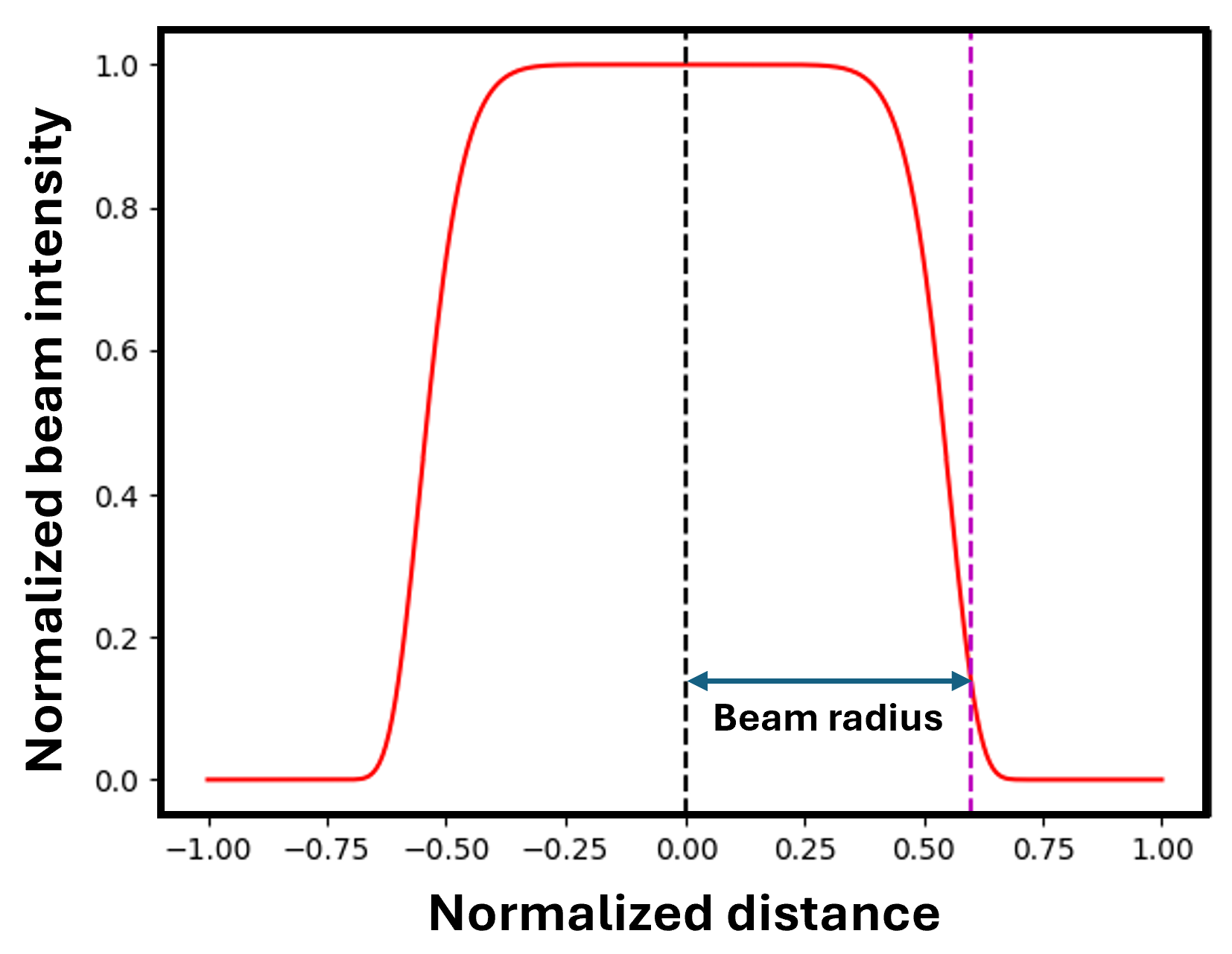
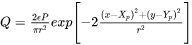About the Heat Source Models
It is crucially important to correctly model the heat source in AM simulations since the heat source not only affects the size of the melt pool but also determines the temperature gradients around the melt pool. In the Additive Manufacturing (AM) Module, these heat source models are available: Gaussian, Core-ring, Top-hat, Double-ellipsoidal, and Conical.
The Configuration window settings for each of these heat sources are further described in both the AM Calculator Conditions Settings and AM Calculator Heat Source Settings topics.
There is a variety of additional background theory topics available.
- The main AM theory is in Additive Manufacturing Module Theory.
- Keyhole model for Gaussian, Core-ring, and Top-hat heat sources: About the Keyhole Model.
- Absorptivity: For Gaussian, Core-ring, and Top-hat heat sources: About the Absorptivity Model.
- Heat source calibrations for Gaussian, Double-ellipsoidal, and Conical heat sources: About Heat Source Calibration.
The Double-ellipsoidal and Conical heat sources are not available with the keyhole model.
The Core-ring and Top-hat heat sources are not available with Heat Source Calibration calculations.
Gaussian Heat Source
The Gaussian model is a surface heat source model which was initially proposed by Pavelic et al. [1969Pav]. By surface heat source model, it is meant that the power input from the heat source is only defined on the top surface of the workpiece, as a Neumann boundary condition on the computational domain, and the heat energy then diffuses into the workpiece depending on the thermal diffusivity of the selected material. As suggested by Pavelic et al., the heat flux (W/m2 ) is defined as Gaussian distribution around the center of the heat source, deposited on the top surface of the domain, as given in the equation below. A schematic representation of the heat flux, as defined by Gaussian heat source is shown in Figure 1.
Where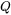 
is the power density deposited on the top surface (W/m2 ),
denotes absorptivity of the laser beam, 
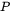is the power of the heat source (W), 
is the laser spot radius, and 
and 
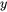denote coordinates of the computational domain while 
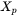and 
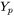represent the location of the heat source.
Also see additional theory related to using a Gaussian heat source with the keyhole option in About the Keyhole Model.
Core-ring Heat Source
Gaussian beam distribution in additive manufacturing often leads to high energy intensity peaks and strong thermal gradients causing manufacturing defects such as keyhole porosity and suboptimal material processing performance. To overcome these challenges, spatial beam shaping is available as an alternate method to customize energy distribution and control the resulting thermal field [2023Bi; 2025Bir]. One of the alternative beam shapes is the Core-ring profile where energy is distributed between a central core and an outer ring.
From a production point of view, the primary benefit of Core-ring and Top-hat beam shapes is that there is a much wider and more stable melt pool. This means that you can increase the productivity of the process so that it prints faster, consequently saving on printing costs [2021Grü].
The alternative beam shape, Top-hat, is described in the next section.
A Core-ring heat source, like a Gaussian heat source, is a surface heat source model, which means that the power input from the heat source is only defined on the top surface of the workpiece, as a Neumann boundary condition. The intensity of a core-ring heat source can be modeled as a combination of a central Gaussian core beam and an outer ring beam [2024Gal].
The intensity of the core beam, as shown in Eq. 1, is given as follows:
[Eq. 2]
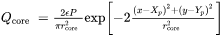
Where
-
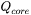is the power density of the Gaussian core (
), -
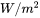denotes the absorptivity of the laser beam, -
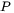is the power of the heat source (W), -
is the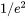 
radius of the core beam, -
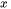and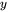 
denote coordinates of the computational domain, and -
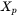and 
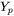represent the location of the heat source.
The intensity of the ring beam is derived by assuming the conservation of the total laser power,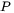 
, and is given as follows:
[Eq. 3]
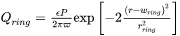
Where
-
is the factor that ensures conservation of the total laser power, -
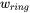is the radial distance of the outer ring beam from the center of the heat source, and -
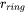is the 
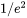radius of the ring beam.
Assuming that the total power remains constant, 
takes the following form:
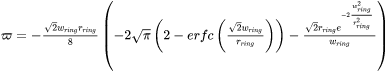
Finally, 
is given as follow:
The total intensity of the core-ring beam is then given as:
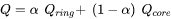
Where 
denotes the fraction of power in the ring beam and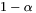 
consequently expresses the fraction of power in the core beam.
Figure 2: A schematic of the intensity profile of a core-ring heat source.
Index Mode (Core-ring)
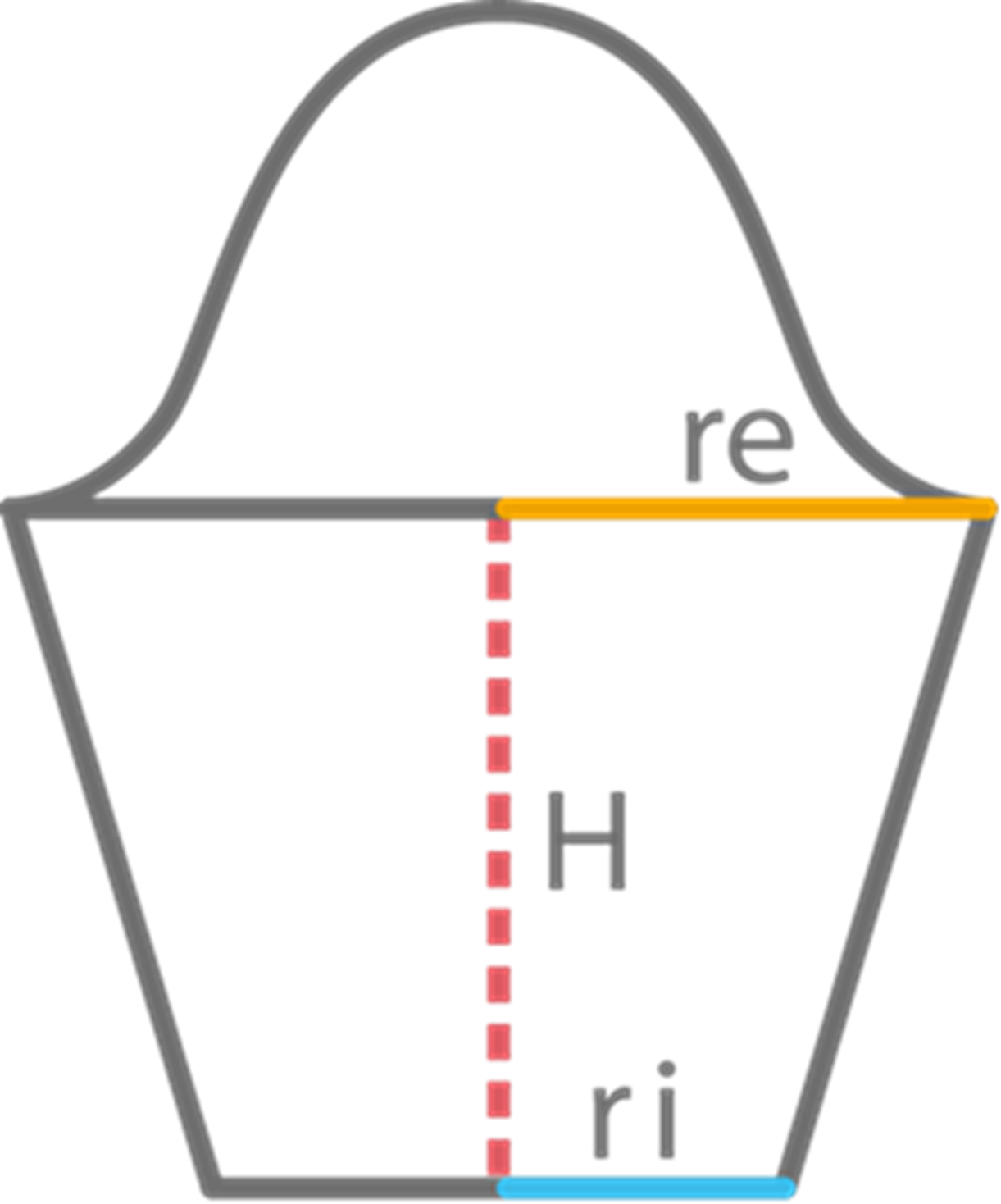
The intensity of the core-ring beam depends on different radii and the distribution of power between the core beam and the ring beam. For most users, these radii are not known since they are selected by the laser optics system of the additive manufacturing (AM) machine being used. The Index Mode is is available with the Core-ring heat source to guide the selection of settings for the Beam radius-Ring, Ring radius, and Amount of power in ring, based on the Beam radius-Core and Index number. The AM Module incorporates configurations commonly provided by AM machines and laser optics systems as described below.
The ratio between the Beam radius-Core and the outer radius i.e. Beam radius-Ring + Ring radius is assumed to be constant and is equal to 0.38. Furthermore, Beam radius-Ring is assumed to be a function of the Beam radius-Core. For instance, for a Beam radius-Core of 50 μm (i.e. diameter of 100 μm), the Beam radius-Ring would be 33 μm and the Ring radius would then be 98.58 μm. Similarly, for Beam radius-Core of 100 μm, the other Beam radii would also scale accordingly, such that the Beam radius-Ring would become 66 μm and the Ring radius would be 197.16 μm.
For the Index Mode, you provide the Beam radius-Core and select the Index number and the rest of the heat source parameters are set as described above.
The Amount of power in ring depends on the selected Index number and is set as follows:
| Index | 0 | 1 | 0 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Amount of power in ring | 7% | 25% | 35% | 50% | 70% | 80% | 90% |
Custom Mode (Core-ring)
The Custom Mode for the Core-ring heat source allows you to manually enter all the parameters of the heat source. This requires an awareness of all the radii, either from the optics system of the AM machine in use, or from the calibration measurements of the laser beam.
If you plan to use the beam radii from the Index Mode but perhaps require a different power distribution in the core/ring, you can first select the Index Mode, enter the Beam radius-Core, then change to Custom Mode and enter the user-defined Amount of power in ring.
Top-hat Heat Source
In addition to the Core-ring beam shape as an alternative to the Gaussian heat source, the Top-hat heat source is available with a flat and uniform energy distribution within a circular region and drops to zero outside the region. A Top-hat heat source is also called a flat-top and is considered a surface heat source model. In the AM Module, the top-hat heat source is approximated with a super-Gaussian beam, which means that the intensity drops to zero gradually within a given distance.
The intensity of such a beam is given as follows [1996Lu]:
[Eq. 4]
Where
-
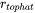is the 
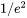radius of the top-hat beam and
-
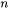is the order of the super Gaussian beam, which determines the steepness of the beam edges. To get a better approximation of the top-hat beam, Thermo-Calc uses 
. -
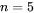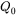is the peak intensity of the top-hat beam, and given the conservation of the total power, it takes the following form:
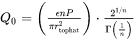
where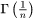 
represents the Gamma function evaluated at 
, 
denotes the absorptivity of the laser beam, and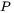 
is the power of the heat source (W).
Figure 3: A schematic of the intensity profile of a top-hat heat source.
Double Ellipsoidal (Goldak) Heat Source
The Double ellipsoidal heat source model is a volumetric heat source model which was first proposed by Goldak et al. [1984Gol], and is now commonly used in LBPF simulations. In contrast to the surface heat source model, in the volumetric heat source model, the power input is defined not only on the surface of the workpiece but also inside the powder bed, along the depth of the powder bed. The heat distribution in the double-ellipsoidal heat source model is given by a combination of two ellipsoids; one in the front quadrant of the heat source and the other in the rear quadrant, as shown in the figure below. The power density is thus given by two different expressions, one for each quadrant of the heat source.
[Eq. 5]
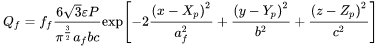
Where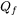 
and 
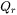are the power densities (W/m3 ) in the front and rear quadrant of the heat source, while 
and 
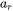are the semi-axes of the front and rear ellipsoids, respectively. 
and 
are the semi-axes along the width and depth of the melt pool.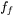 
and 
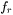are the proportional coefficients for the front and rear ellipsoid of the heat source, with the condition 
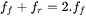is then given as follows:
[Eq. 6]
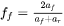
Conical Heat Source
The Conical heat source model is also a volumetric heat source model, which was first employed for welding simulations but due to inherent similarities between welding and LPBF processes, this model is also commonly used for AM simulations. The conical heat source model is defined by a Gaussian heat distribution on the top surface of the workpiece and a conical distribution along the depth of the powder bed. A schematic representation of the energy distribution for conical heat source model is shown below.
The power density for the conical heat source is given as follows [2019Zha]:
[Eq. 7]
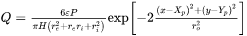
with
where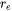 
and 
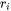are the cone radius at the top and bottom, respectively, while 
is the height of the cone.
References
[1969Pav] V. Pavelic, Experimental and computed temperature histories in gas tungsten arc welding of thin plates. Weld. J. Res. Suppl. 48, 296–305 (1969).
[1984Gol] J. Goldak, A. Chakravarti, M. Bibby, A new finite element model for welding heat sources. Metall. Trans. B. 15, 299–305 (1984).
[1996Lu] B. Lü, B. Zhang, X. Wang, Three-dimensional intensity distribution of focused super-Gaussian beams. Opt. Commun. 126, 1–6 (1996).
[2019Zha] Z. Zhang, Y. Huang, A. Rani Kasinathan, S. Imani Shahabad, U. Ali, Y. Mahmoodkhani, E. Toyserkani, 3-Dimensional heat transfer modeling for laser powder-bed fusion additive manufacturing with volumetric heat sources based on varied thermal conductivity and absorptivity. Opt. Laser Technol. 109, 297–312 (2019).
[2021Grü] J. Grünewald, F. Gehringer, M. Schmöller, K. Wudy, Influence of Ring-Shaped Beam Profiles on Process Stability and Productivity in Laser-Based Powder Bed Fusion of AISI 316L. Metals (Basel). 11, 1989 (2021).
[2023Bi] J. Bi, L. Wu, S. Li, Z. Yang, X. Jia, M. D. Starostenkov, G. Dong, Beam shaping technology and its application in metal laser additive manufacturing: A review. J. Mater. Res. Technol. 26, 4606–4628 (2023).
[2024Gal] F. Galbusera, L. Caprio, B. Previtali, A. G. Demir, Analytical modeling and characterization of ring beam profiles for high-power lasers used in industrial manufacturing. J. Manuf. Process. 117, 387–404 (2024).
[2025Bir] M. Birg, T. Novotny, F. Bayer, “Beam Shaping in Additive Manufacturing A Toolbox of New Possibilities (White paper)” (2025); https://www.eos.info/content/blog/entering-the-next-era-of-am-with-beam-shaping.