About the Absorptivity Model

The absorptivity of a flat metal surface is a function of the alloy composition, temperature, the wavelength of the heat source, and the angle of incidence.

The absorptivity of a metallic powder is more complex. Most metallic powders are oxidized at the surface where a thin layer of oxide often increases absorptivity. Multiple reflections of the laser rays also increases the effective absorptivity, e.g. at surface roughness or between the particles within the powder layer. The additional complications of the metallic powder are neglected in this model, which focuses on an ideal flat surface of the liquid phase after the powder has melted. This simplification can be justified at steady-state conditions when a melt pool is established and most laser rays hit the liquid surface in the melt pool.

Additional related theory topics include: Additive Manufacturing Module Theory, About the Heat Source Models, and About the Keyhole Model.

Laser Beam Reflection

A fraction of the energy of a laser ray (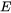) is absorbed when it strikes a surface, the rest of the energy is reflected (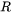), i.e. the absorptivity is given by .

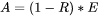The Fresnel equation describes how the absorptivity depends on the angle of incidence .

For an unpolarized laser beam, the reflection coefficient 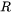is the average of the parallel and perpendicular component, denoted by 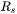and :

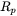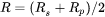
Both components of 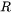are given by the Fresnel equations:

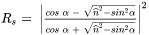
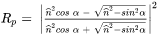
The refraction index 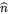is a complex number 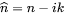where 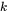corresponds to the extinction coefficient.

The refractive index is directly related to the electric permittivity, :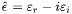

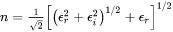
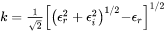
About the Lorentz-Drude (LD) Model

The Lorentz-Drude model (LD) relates the electric permittivity with the electric resistivity [2021Yan].

The electric resistivity thermophysical property is included in many Thermo-Calc databases. For a list of databases that include it, see the Properties that Can Be Calculated brochure on the website or refer to the specific database documentation.

The LD model only considers the intraband absorption and is neglecting the interband part. The interband part of absorption is, however, often less dominant for wavelengths larger than 1 μm; for smaller wavelengths the model shows larger deviations when compared to experimental data.

For additive manufacturing lasers, the most common wavelength used is 1.06 μm.

The LD model is used as a first approximation of the dielectric constants of an alloy. The model is then further calibrated against the available experimental information of dielectric constants, refraction index, and absorptivity of liquid metal, i.e. the correction functions 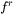and 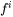are modeled:

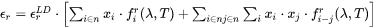
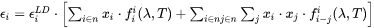
where

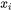• is the mole-fraction of element
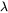• the laser wavelength, and
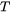• the temperature.

The correction improves the model accuracy for the entire wavelength spectrum.  

Following the work by Yang [2021Yan], the LD model obtains the real and imaginary parts of the electric permittivity:

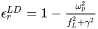
where

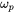• is the plasma frequency,
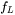• is the laser frequency, and
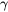• is the damping frequency.

The plasma frequency is given by:

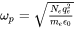
where

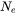• is the number density of free electrons,
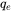• the absolute value of elementary charge, ,
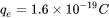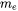• is the electron mass, 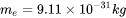, and
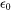• is the vacuum permittivity,  .

The damping frequency can be expressed as:

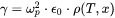
where

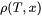• is the temperature- and composition-dependent electrical resistivity.

The laser frequency can be expressed as:

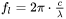
where

• is the speed of light in vacuum, and
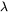• is the wavelength of the laser.

The free electron density 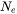is assumed to be given directly by the atomic mass and mass density:

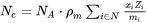
where

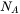• is the Avagadros constant,
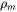• is the mass density of the alloy,
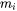• is the atomic weight of element , and
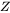• is the number of valence electrons per atom of element .

Heat Sources and Absorptivity

The LD model for liquid absorptivity describes a material property and is applicable to the Gaussian, Core-ring, and Top-hat heat sources where the energy is added to the surface of the material.

The LD model for absorptivity is not applicable to the volume heat sources Double ellipsoidal and Conical. Volume heat sources assume an effective absorptivity that indirectly can include the effect of keyholing by increasing the absorptivity as a function of energy density.

Surface Heat Sources

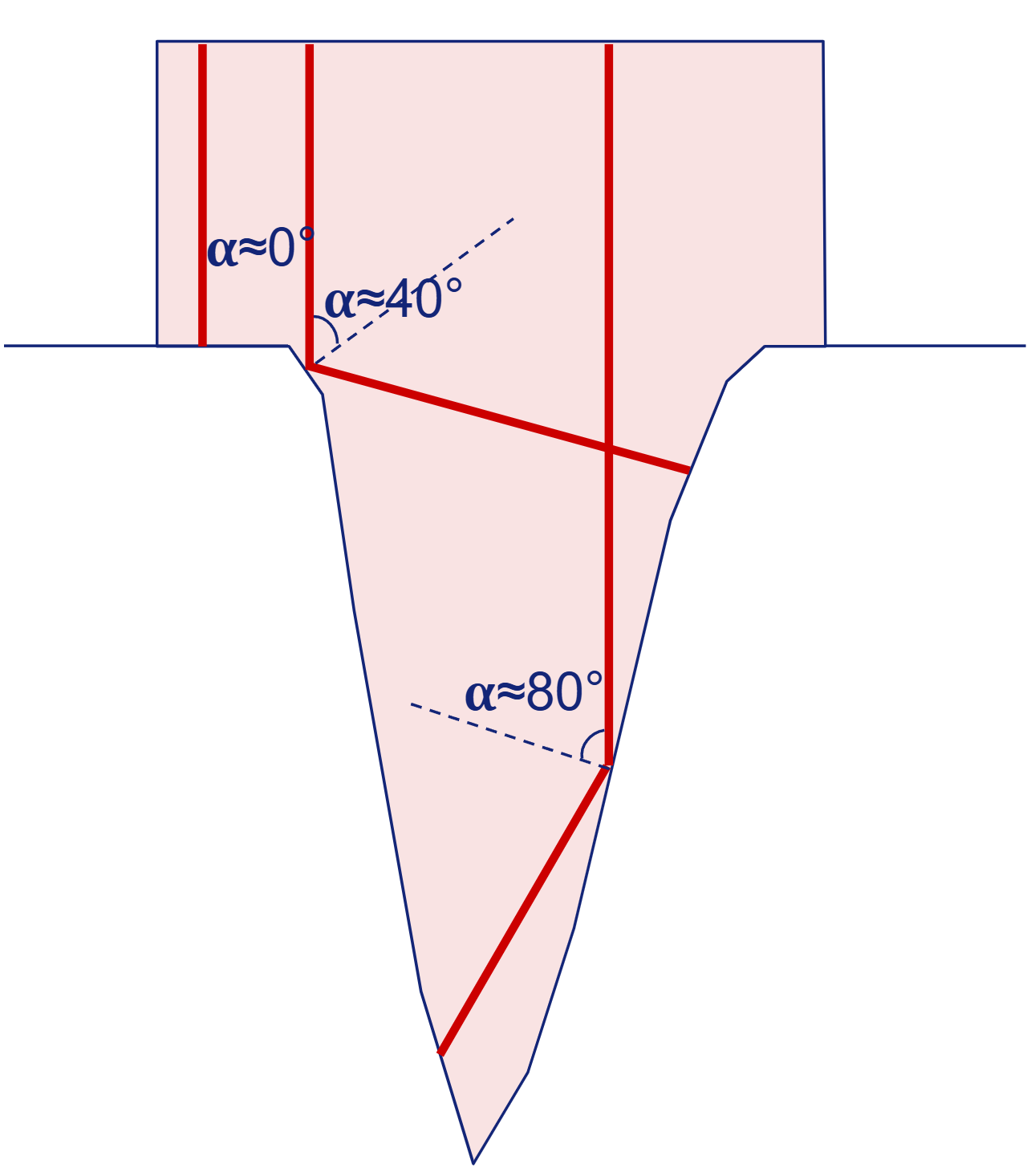
The angle of incidence for a laser ray is zero when no keyhole forms. The angle of incidence varies greatly within the keyhole and the full angle dependent absorptivity model is used.

The absorptivity model takes the wavelength of the heat source as input together with a prefactor that can scale the calculated absorptivity up or down. The scaling can be required to calibrate the simulations against experiments.

The following absorptivity settings are described in the AM Calculator Heat Source Settings. The examples use Gaussian, but Core-ring and Top-hat area also available.

The resulting absorptivity (given the wavelength and prefactor) can be visualized from the Material Properties tab on the AM Calculator Configuration window.

The following absorptivity options are described in AM Calculator Heat Source Settings.

From the Plot list, select:

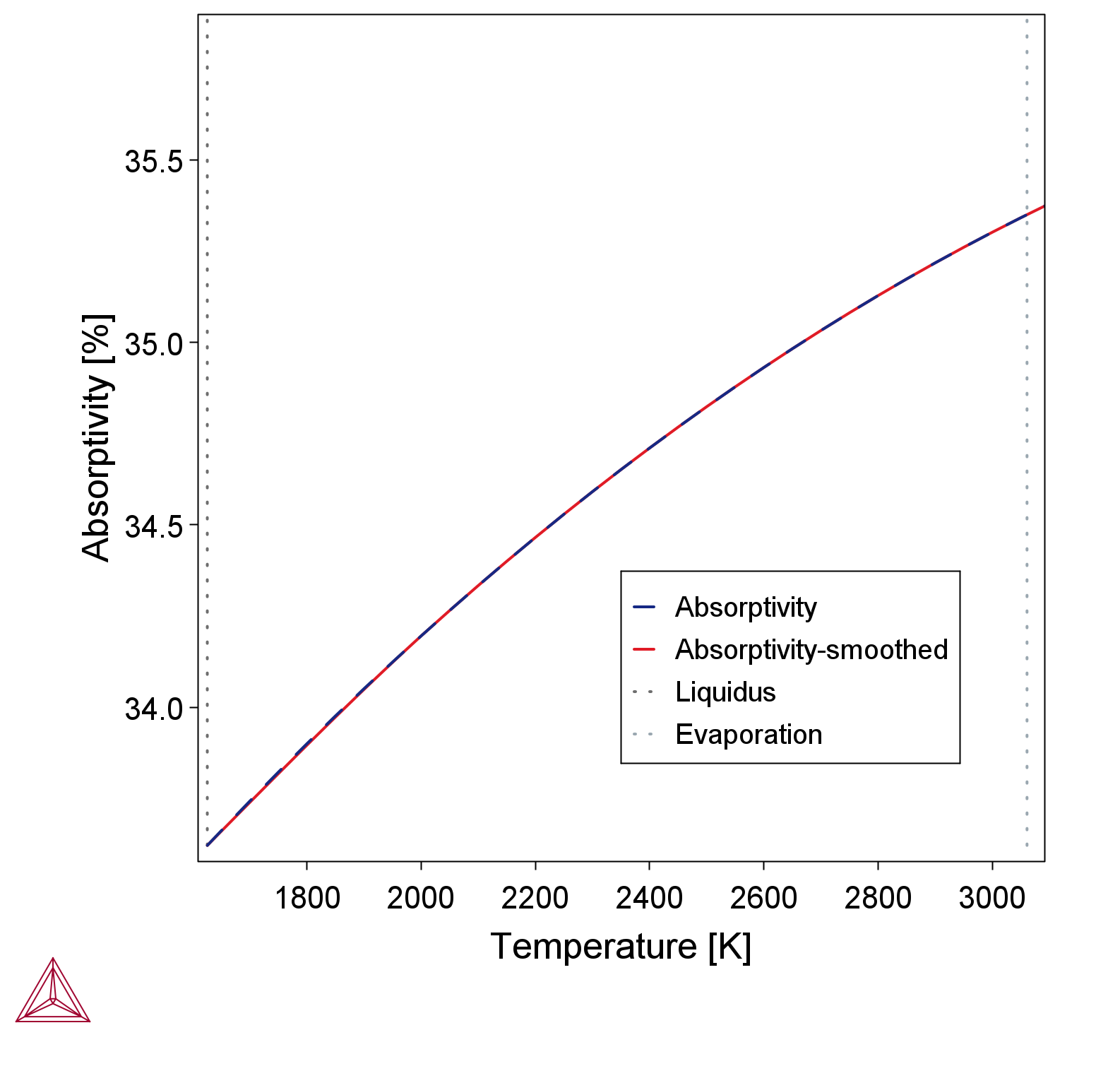
• Absorptivity to visualize the temperature dependent absorptivity for the liquid phase of the selected material (Figure 5).
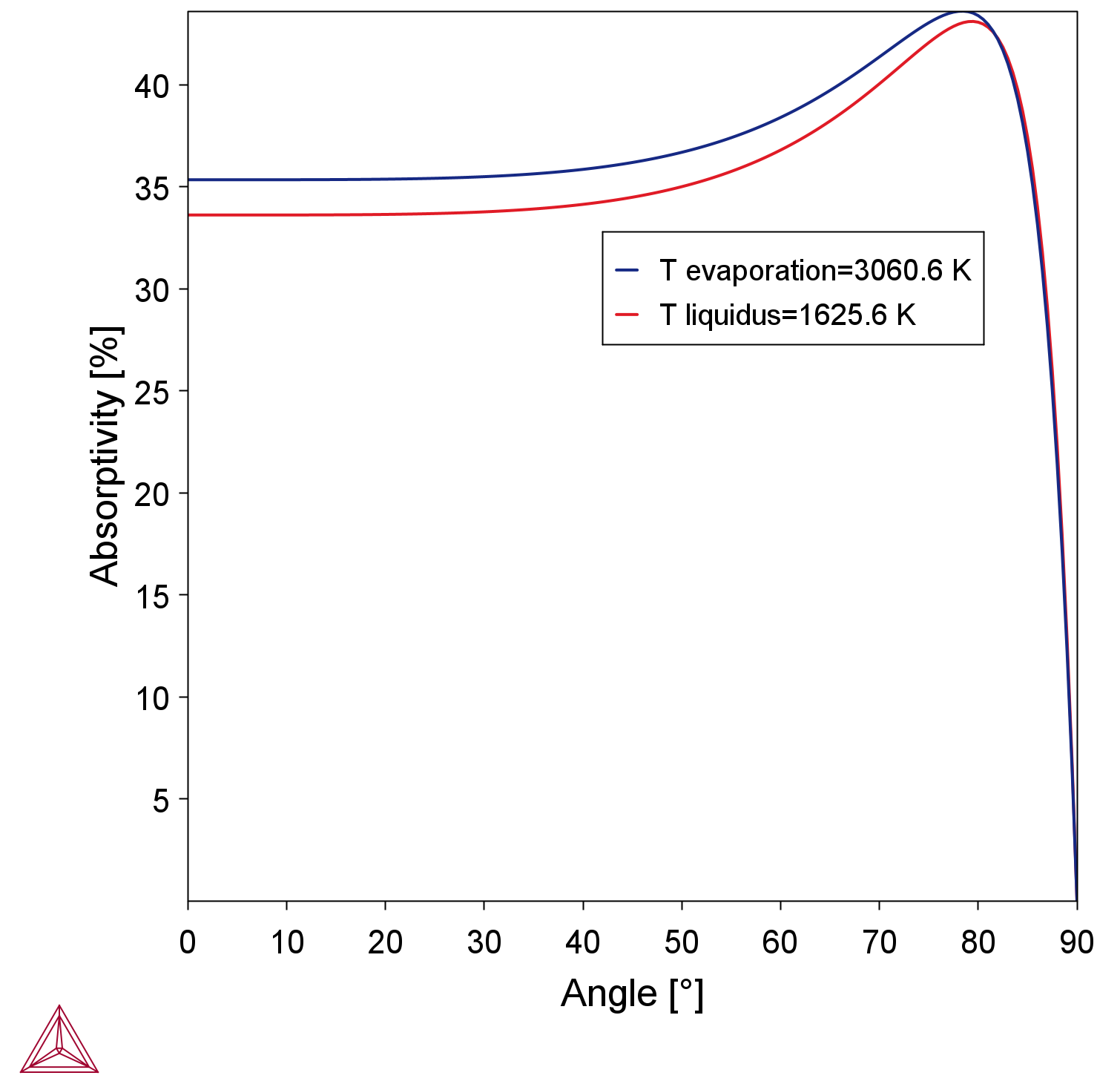
• Absorptivity vs angle to visualize the angle dependent absorptivity at liquidus and the evaporation temperature (Figure 6).  
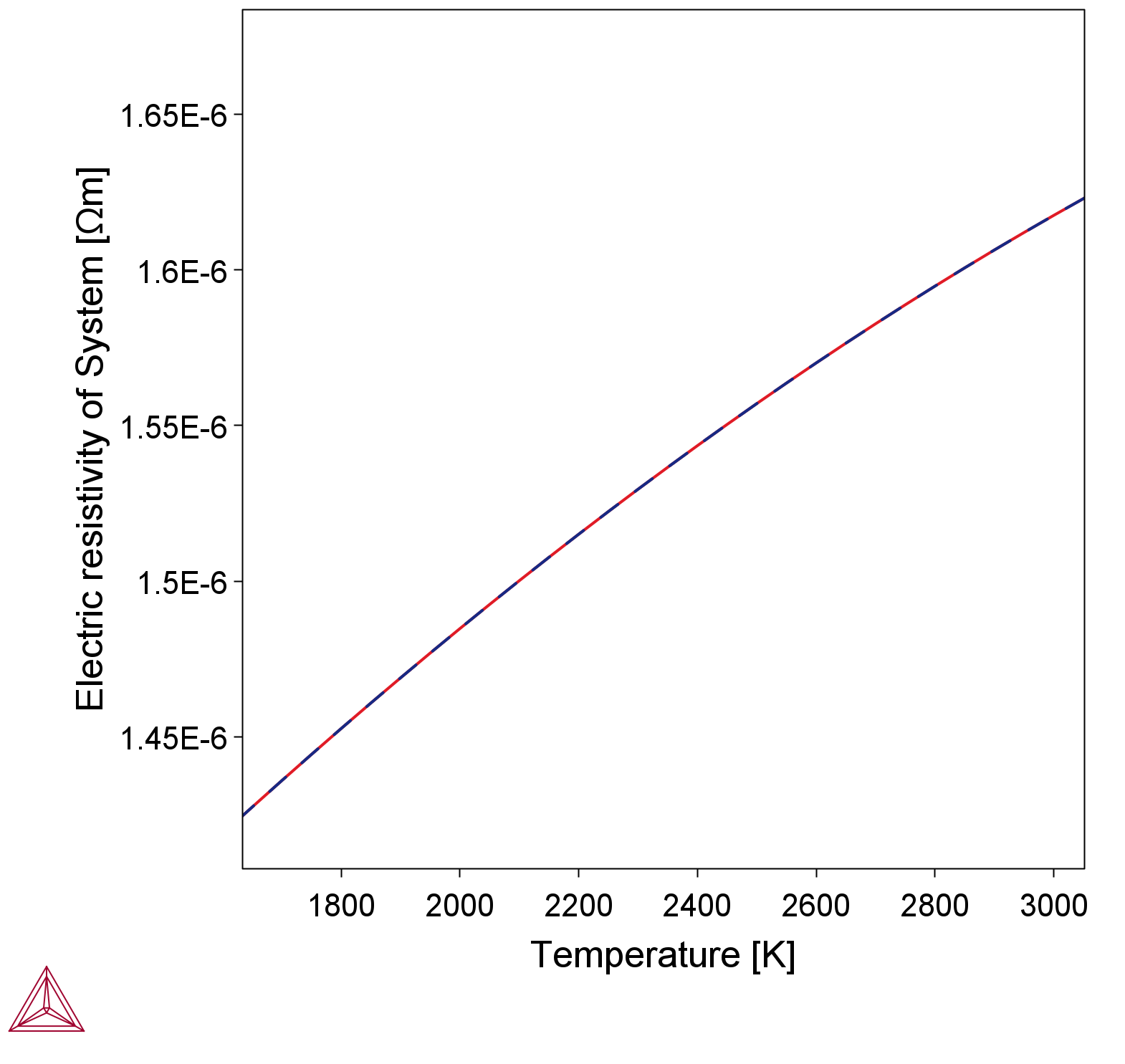
• Electric resistivity to visualize it as a function of temperature (Figure 7).

  The electric resistivity is not directly used in the AM simulations, only indirectly through the absorptivity model that uses the electric resistivity when modeling the composition, temperature, and angle dependent absorptivity.

Figure 7: The electric resistivity of the liquid phase for the alloy IN738LC. The electric resistivity is used in the model for absorptivity for the liquid phase.

Heat Source Calibration

Additional settings are described in the AM Calculator Conditions Settings topic.

AM_06a: Calibrating a Heat Source for a 316L Steel

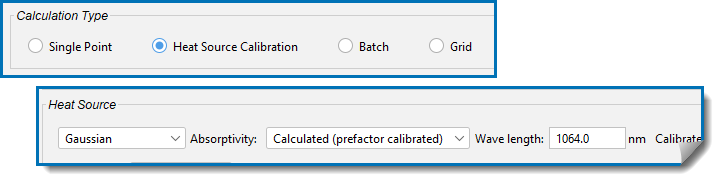
For Gaussian Heat Source Calibration calculations, you can use the temperature and angle dependent calculated absorptivity and calibrate the scaling prefactor to match the given experimental data. The settings are on the AM Calculator Configuration window. 

For Absorptivity select Calculated (prefactor calibrated) then enter the Wavelength of the heat source or use the default value.

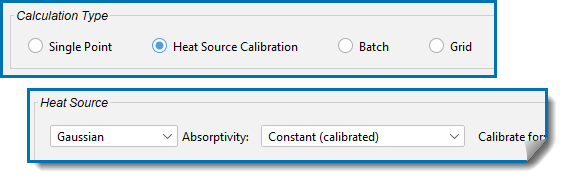
In order to use a constant Absorptivity, you can instead select Constant (calibrated), which uses a constant value of absorptivity i.e. it is not dependent on temperature or incidence angle. Then you can calibrate that value to match the given experimental data.

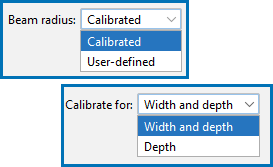
For both Absorptivity options (Calculated (prefactor calibrated) or Constant (calibrated)) you can also either calibrate the Beam radius along with the absorptivity or the prefactor (choose Calibrated), or use a fixed value of Beam radius and calibrate only the absorptivity (choose User-defined).

Another setting available with the Gaussian Heat Source Calibration, is to calibrate for both the Width and depth of the melt pool from the experimental data or use only the Depth of the melt pool for the calibration. If you choose Width and depth, the Experiment Data values in the table require both the width and depth of the melt pool whereas if you only calibrate the depth then the data file needs to only include the information for the depth of the melt pool.

Reference

[2021Yan] Z. Yang, A. Bauereiß, M. Markl, C. Körner, Modeling Laser Beam Absorption of Metal Alloys at High Temperatures for Selective Laser Melting. Adv. Eng. Mater. 23, 2100137 (2021).