Theory for the Multiphase Simulation

More details about the homogenization model for multiphase simulations can be found in Larsson and Engström [2006Lar] and Larsson and Höglund [2009Lar]. As mentioned in the description of this simulation, it is assumed that the material is locally fully equilibrated and that the local phase fractions, phase compositions and so forth are obtained from an equilibrium calculation with the local overall composition as a condition. From a numerical point of view the homogenization model treats the multiphase material as a single phase having the “average”, or “effective”, properties of the local phase mixture.

When estimating the effective kinetics of a multiphase mixture the product of solubility and mobility in each phase is considered. It is therefore convenient to define

When estimating the effective kinetics of a multiphase mixture the product of solubility and mobility in each phase is considered, define this for each phase

for each phase ɸ. The effective kinetics of the multiphase mixture is denoted and in this example it was evaluated using the lower Hashin-Shtrikman bound. The default method is a simple rule of mixtures

The default method is a simple rule of mixtures

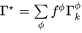
where 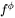$volume fraction of f^\phi$ is the volume fraction of ɸ. The flux is obtained as

The flux is obtained as this

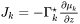
which replaces the single-phase equation

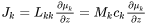
for multiphase simulations.

References

[2006Lar] H. Larsson, A. Engström, A homogenization approach to diffusion simulations applied to α+γ Fe–Cr–Ni diffusion couples. Acta Mater. 54, 2431–2439 (2006).

[2009Lar] H. Larsson, L. Höglund, Multiphase diffusion simulations in 1D using the DICTRA homogenization model. Calphad 33, 495–501 (2009).