Theory for the Single Phase Simulation
The flux of a component  in the z-direction in an isobarothermal system is in general given by
in the z-direction in an isobarothermal system is in general given by
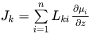
where  is a matrix of kinetic coefficients and
is a matrix of kinetic coefficients and 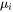 is the chemical potential of component
is the chemical potential of component  . The correlation effects, i.e. the coupling of the flux of
. The correlation effects, i.e. the coupling of the flux of 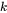 component to the chemical potential gradients of the other elements, are normally neglected
component to the chemical potential gradients of the other elements, are normally neglected
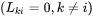
and thus
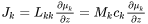
where 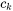 is the concentration and
is the concentration and 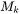 the mobility of component
the mobility of component 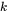 .
.
The equation for the flux is combined with the equation of continuity, which takes the following form in a planar domain,
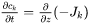
which relates the local evolution of the concentration of 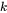 to the divergence of the flux.
to the divergence of the flux.
The expression for the flux can be expanded in terms of concentration gradients
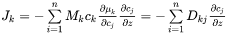
where the diffusion coefficient of component 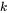 with respect to the concentration gradient of component
with respect to the concentration gradient of component 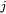 has been introduced.
has been introduced.
The flux expressions above are given in the so-called lattice-fixed frame of reference. In practical calculations it is more common to use a volume-fixed frame of reference. For a discussion of these concepts, see Andersson and Ågren [1992And].
Reference
[1992And] J.-O. Andersson, J. Ågren, Models for numerical treatment of multicomponent diffusion in simple phases. J. Appl. Phys. 72, 1350–1355 (1992).