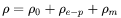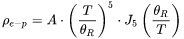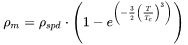Electrical Resistivity Model
The modeling starts with unaries in their stable and metastable structures. The temperature dependence of electrical resistivity is described with polynomials for each unary and each end-member of compounds. In order to guarantee the reliability of the extrapolation, experimental data were first fitted to a semi-empirical model, which was established based on relevant theories. The experimental data, together with the extrapolated values, are then used for deriving the polynomials that are saved in the database. The magnetic contribution to electrical resistivity can be separately treated with a model implemented in Thermo-Calc.
The composition dependence of electrical resistivity is described with the Redlich-Kister expression. All binary systems are modeled by using experimental data or theoretical estimations. Ternary and higher-order parameters can be used if necessary.
Electrical resistivity is modeled and its descriptions are stored in the databases. Electrical conductivity is derived from electrical resistivity and can be retrieved from calculated results as well.
The semi-empirical model for electrical resistivity is built based on the Matthiessen’s rule [1997DeB]. In general, the electrical resistivity of a metallic alloy consists of residual resistivity (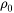 ) and electron-phonon resistivity (
) and electron-phonon resistivity ( ), as well as magnetic resistivity (
), as well as magnetic resistivity (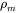 ). The residual resistivity is due to the scatterings of impurities and defects that exist in well-annealed and high purity alloys, and the value of
). The residual resistivity is due to the scatterings of impurities and defects that exist in well-annealed and high purity alloys, and the value of 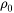 is generally considered independent of temperature.
is generally considered independent of temperature.
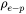 is described with the modified Bloch-Grüneisen equation [1928Blo; 1933Gru] and corrections can be made in cases where other types of scatterings play considerable roles.
is described with the modified Bloch-Grüneisen equation [1928Blo; 1933Gru] and corrections can be made in cases where other types of scatterings play considerable roles.
[Eq. 3]
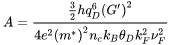
[Eq. 4]
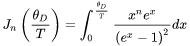
The characteristic temperature 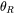 plays a similar role and is also approximated as the Debye temperature (
plays a similar role and is also approximated as the Debye temperature ( ), which can be readily obtained from low-temperature heat capacity and elastic constants data as well as theoretical computations. The approximation of
), which can be readily obtained from low-temperature heat capacity and elastic constants data as well as theoretical computations. The approximation of 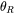 as
as 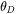 indicates that transverse phonons play a role in electron scattering.
indicates that transverse phonons play a role in electron scattering. 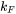 is the electron wave number at the Fermi surface.
is the electron wave number at the Fermi surface.  is the phonon Debye wave number.
is the phonon Debye wave number. 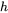 is the Planck constant.
is the Planck constant. 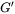 is a constant representing the strength of the e-p interaction and cannot be easily estimated.
is a constant representing the strength of the e-p interaction and cannot be easily estimated. 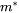 is the electron effective mass.
is the electron effective mass. 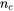 is the number of unit cells per unit volume.
is the number of unit cells per unit volume. 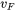 is the electron velocity at the Fermi surface.
is the electron velocity at the Fermi surface.
To describe the drastic change of the magnetic resistivity (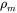 ) around the Curie (or Neel) temperature,
) around the Curie (or Neel) temperature, 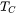 , of a magnetic alloy, an empirical model is proposed using the dimensionless temperature
, of a magnetic alloy, an empirical model is proposed using the dimensionless temperature 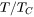 and a parameter
and a parameter 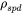 that stands for the resistivity due to spin disordering. According to this model, Eq. 5,
that stands for the resistivity due to spin disordering. According to this model, Eq. 5, 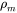 approaches
approaches 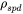 , when the temperature is well above
, when the temperature is well above 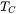 , and is 0 when the temperature is far below
, and is 0 when the temperature is far below 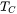 .
.  depends only on composition and is described with the Redlich-Kister (R-K) expression. Apparently,
depends only on composition and is described with the Redlich-Kister (R-K) expression. Apparently, 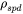 has a positive value for magnetic elements, and compounds as well as endmembers, and is 0 for non-magnetic ones.
has a positive value for magnetic elements, and compounds as well as endmembers, and is 0 for non-magnetic ones.
In a typical binary system made of a magnetic element A and a non-magnetic element B, 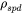 decreases usually from
decreases usually from 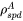 to 0 at a certain composition (
to 0 at a certain composition (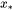 ). Such a behavior is also seen in magnetic moment and Curie temperature.
). Such a behavior is also seen in magnetic moment and Curie temperature.  is expected to be zero in the composition range from
is expected to be zero in the composition range from 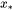 to element B, and will be forced to zero when the R-K expansion leads inevitably to negative values over this composition range.
to element B, and will be forced to zero when the R-K expansion leads inevitably to negative values over this composition range. 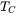 is available from the thermodynamic description in the database.
is available from the thermodynamic description in the database.
The semi-empirical model (as given in Eq. 1 to Eq. 5) is first fitted to experimental data. The description is then extrapolated to a wider temperature range if necessary, either to extreme temperatures where the structure is no longer stable or to where experimental data are missing. Polynomials are then derived with the experimental data, together with the extrapolated values, and stored in the database. The model as given in Eq. 5 is implemented in Thermo‑Calc, so the magnetic contribution can be excluded from the polynomials and separately modeled, and it will be automatically included during the calculations.
The extended TDB format accepts parameters describing electrical resistivity and thermal conductivity, together with spin disordering resistivity. Examples for unary and binary systems are given below:
ELRS(FCC_A1,AL:VA;0)
ELRS(FCC_A1,AL,CO:VA;0)
ESPD(FCC_A1,CO:VA;0)
ESPD(FCC_A1,AL,CO:VA;0)
ELRS– Electrical resistivityELCD– Electrical conductivity
All the above quantities can be calculated, retrieved, shown and plot in Thermo‑Calc via the variables in the Console Mode or via the quantity names in the Graphical Mode (see sections below).
The quantities corresponding to the variables of ELRS and ELCD can be calculated in Console Mode for a phase, e.g. ELRS(FCC_A1), or for a system, i.e. ELRS. The results can be shown in the POLY module with the command SHOW_VALUE or illustrated as a plot in the POST module with the command PLOT_DIAGRAM.
On the Plot Renderer in Graphical Mode, electrical resistivity, electrical conductivity, thermal conductivity, thermal resistivity, and thermal diffusivity can be selected from the axes lists, tabulated and plotted using the quantity names, with options for a specific phase, all phases or for a system.
With these Software Development Kits (SDKs), the quantities of ELRS and ELCD can be retrieved, for a phase, e.g. ELRS(FCC_A1), or for a system, i.e. ELRS, via get_value_of() or get_values_of(), from most phase equilibrium calculations in TC-Python, for instance,
with_single_equilibrium_calculation(),with_property_digram_calculation()orwith_batch_equilibrium_calculation().
These can also be accessed in both ThermodynamicQuantity and ScheilQuantityclasses. You can, for example, use ThermodynamicQuantity.electrical_resistivity() for electrical resistivity.
[1928Blo] F. Bloch, Über die Quantenmechanik der Elektronen in Kristallgittern (About the quantum mechanics of electrons in crystal lattices). Zeitschrift fur Phys. 52, 555–600 (1928).
[1933Gru] E. Grüneisen, The dependence of the electrical resistance of pure metals on the temperature. Ann. Phys. 16, 530–540 (1933).
[1997DeB] R. De-Bruyn-Ouboter, Heike Kamerlingh Onnes’s discovery of superconductivity. Sci. Am., 98–103 (1997).