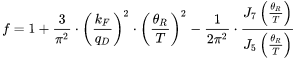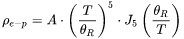Thermal Conductivity Model

The modeling starts with unaries in their stable and metastable structures. The temperature dependence of thermal conductivity is described with polynomials for each unary and each end-member of compounds. Thermal resistivity and thermal diffusivity can be derived from thermal conductivity and retrieved from calculated results. The composition dependence is described with the Redlich-Kister expression in the CALPHAD spirit, but the relation is applied to thermal resistivity (or the inverse of thermal conductivity).

Experimental data of thermal conductivity are used to derive descriptions in polynomials, which are stored in the database, despite that it consists of two components, electronic thermal conductivity (electronic thermal conductivity) and lattice thermal conductivity lattice thermal conductivity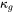. In other words, they are not separately treated.

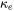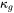In cases where experimental data are absent or sparse, however, electronic thermal conductivity and lattice thermal conductivity can be separately predicted and summed up to give the total thermal conductivity. electronic thermal conductivity 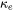can be predicted from 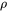resistivity or vice versa, by employing the Wiedemann-Franz Law [1853Fra; 1985Jon], respectively, to the residual resistivity, magnetic resistivity and intrinsic resistivity.

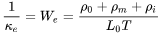
[Eq. 1]          Equation 6

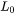Sommerfeld value is known as the Sommerfeld value of the Lorenz number: Lorenz number.

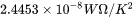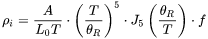
[Eq. 2]          Equation 7

[Eq. 3]          Equation 8

The intrinsic resistivity ( intrinsic resistivity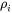) is based on Eq. 4

[Eq. 4]          Equation 2

for the e-p processes, but corrections are provided, as given in Eq. 3: the first term corresponds to large-angle scattering that satisfies the original Wiedemann-Franz Law; the second one is due to inelastic small-angle (vertical processes) and has no counterpart in the electrical resistivity; the third term is a correction that accounts for situations where large-angle scattering can reverse the electron direction without actually assisting to restore the distribution back to equilibrium.

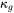lattice thermal conductivity can be predicted with the Slack model in a temperature range where only anharmonic Umklapp phonon-phonon interactions are important. In other words, normal processes are neglected as a first approximation [1979Sla; 2002Mor]. The most reasonable version among several ones is given below [1965Jul].

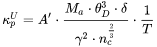
[Eq. 5]          Equation 9

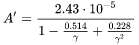
[Eq. 6]          Equation 10

The Debye temperature, Debye temperature 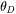can be obtained from low-temperature heat capacity or elastic constant data. 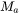average atomic mass is the average atomic mass, 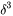volume per atom 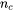the volume per atom, number of atoms in a unit cell the number of atoms in a unit cell, and 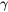Grüneisen coefficient the Grüneisen coefficient. 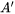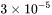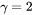A typical value for A prime is evaluated to be 3 times 10 to the -5 using Grüneisen coefficient as the Grüneisen coefficient, and can be used in the absence of experimental information. It can also be obtained from e.g. DFT calculations of elastic properties.

The extended TDB format accepts parameters describing electrical resistivity and thermal conductivity, together with spin disordering resistivity. Examples for unary and binary systems are given below:

THCD(FCC_A1,AL:VA;0)

THCD(FCC_A1,AL,CO:VA;0)

  • THCD – Thermal conductivity
  • THRS – Thermal resistivity
  • THDF – Thermal diffusivity

All the above quantities can be calculated, retrieved, shown and plot in Thermo‑Calc via the variables in the Console Mode or via the quantity names in the Graphic Mode (see sections below).  

The quantities corresponding to the variables of THCD, THRS, and THDF can be calculated in Console Mode for a phase, e.g. THCD(FCC_A1), or for a system, i.e.  THCD. The results can be shown in the POLY module with the command SHOW_VALUE or illustrated as a plot in the POST module with the command PLOT_DIAGRAM.

On the Plot Renderer in Graphical Mode, electrical resistivity, electrical conductivity, thermal conductivity, thermal resistivity, and thermal diffusivity can be selected from the axes lists, tabulated and plotted using the quantity names, with options for a specific phase, all phases or for a system.

The quantities of THCD, THRS, and THDF can be retrieved, for a phase, e.g. THCD(FCC_A1), or for a system, i.e.  THCD, via get_value_of() or get_values_of(), from most phase equilibrium calculations in these Software Development Kits (SDKs), for instance,

  • with_single_equilibrium_calculation(),
  • with_property_diagram_calculation() or
  • with_batch_equilibrium_calculation().

These can also be accessed in both ThermodynamicQuantity and ScheilQuantity classes. You can, for example, use ThermodynamicQuantity.thermal_resistivity() for thermal resistivity.

[1852Fra] R. Franz, G. Wiedemann, Ueber die Wärme-Leitungsfähigkeit der Metalle. Ann. der Phys. und Chemie. 165, 497–531 (1853).

[1965Jul] C. L. Julian, Theory of Heat Conduction in Rare-Gas Crystals. Phys. Rev. 137, A128–A137 (1965).

1979[Sla] G. A. Slack, The Thermal Conductivity of Nonmetallic Crystals, in Solid State Physics Volume 34, 1–71 (1979).

[1985Jon] W. Jones, N. H. March, Theoretical Solid State Physics (Courier Dover Publications, 1985).

[2002Mor] D. T. Morelli, J. P. Heremans, G. A. Slack, Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III-V semiconductors. Phys. Rev. B. 66, 195304 (2002).