About the Elastic Properties
As of Thermo-Calc version 2025b, elastic properties are available with Thermo‑Calc and the TCS Ti/TiAl-based Alloys Database (TCTI) (TCTI6 and newer), TCS Steel and Fe-alloys Database (TCFE) (TCFE14 and newer), TCS High Entropy Alloys Database (TCHEA) (TCHEA8 and newer), and TCS Ni-based Superalloys Database (TCNI) (TCNI13 and newer). These elastic properties will be added to additional databases over time. Subscribe to our newsletter to be kept up-to-date on the latest product releases, webinars, user group meetings, applications examples, and more.
To use the elastic properties parameters, the database parameter ECij is needed. The elastic stiffness tensor is described by its independent tensor elements (elastic constants) given by the indices 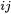 in Voigt notation. Both indices
in Voigt notation. Both indices  and
and 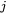 run from 1 to 6 and the number of independent tensor elements depends on the symmetry of the crystal lattice (i.e., three independent constants for cubic crystals and five for hexagonal crystals). The elastic moduli are derived from the elastic constants.
run from 1 to 6 and the number of independent tensor elements depends on the symmetry of the crystal lattice (i.e., three independent constants for cubic crystals and five for hexagonal crystals). The elastic moduli are derived from the elastic constants.
Elastic properties are only available for cubic (FCC and BCC) or hexagonal (HCP) phases.
Elastic Properties Model
The modeling process begins with determining the independent elastic constants for each phase.
- For cubic (FCC, BCC) phases, the independent elastic constants are:
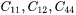 .
. - For hexagonal (HCP) phases, the independent elastic constants are:
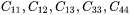 .
.
The temperature dependence of the elastic constants is represented by exponential and polynomial functions for each phase's end-member. To ensure reliable interpolation and extrapolation, both experimental and theoretical data are fitted to a robust model based on relevant theories, following the CALPHAD methodology. For magnetic materials, the magnetic contribution to the elastic constants is treated separately and incorporated into the model implemented in Thermo-Calc [2021Joh].
The elastic constants assessed for single crystalline phases are related to the polycrystalline elastic moduli (bulk, shear, and Young’s moduli) using the Voigt-Reuss-Hill averaging method. These moduli are expressed in terms of the Voigt (upper bound) and Reuss (lower bound) limits of the elastic moduli as follows:
Bulk modulus
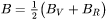
Shear modulus

Young's modulus
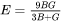
Cubic Symmetry
The Voigt and Reuss bounds depend on crystal symmetry. For cubic (FCC, BCC) phases with 3 independent elastic constants (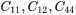 ), the Voigt and Reuss bounds are given as:
), the Voigt and Reuss bounds are given as:
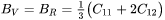
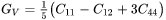
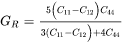
Hexagonal Symmetry
For hexagonal (HCP) phase with 5 independent elastic constants (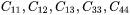 ), the Voigt and Reuss bounds are calculated as:
), the Voigt and Reuss bounds are calculated as:
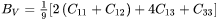
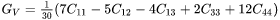
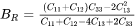
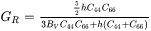
Where the symmetry relation 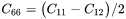 and help function
and help function 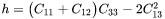 are used to further condense
are used to further condense 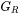 .
.
The CALPHAD Method and the Thermo‑Calc Databases. Also visit the video tutorials on our website or our YouTube playlist.
Model Parameters
The extended TDB format accepts parameters describing elastic constants and magnetic ordering effects. Examples for unary and binary systems are given below for C11:
EC11(HCP_A3,TI:VA;0)
EC11(HCP_A3,TI,MO:VA;0)
EC11(BCC_A2,FE:VA;0)
EC11MAG(BCC_A2,FE:VA;0)
EC11(BCC_A2,FE,CR:VA;0)
Where EC11MAG is the scaling factor for the magnetic contribution.
Calculation and Plot Variables
- Elastic constants (Cij)
- Bulk modulus
- Shear modulus
- Young’s modulus
All of the above quantities can be calculated, retrieved, shown, and plotted in Thermo‑Calc via the variables in Console Mode or via the axes quantity names in Graphical Mode.
In the Plot Renderer in Graphical Mode, elastic constants and moduli can be selected from the drop-down list of axis variables.
The independent elastic constants are selected on the Plot Renderer as an axis variable Elastic constant and then choose an option (C11, C12, C13, C33, or C44) from the drop-down list.
The elastic moduli, Bulk modulus, Shear modulus, and Young's modulus, are directly available from the Axis variable list.
All can be tabulated and plotted using the quantity names, with options for a specific phase or all phases.
The quantities corresponding to the individual elastic constants and elastic moduli (derived from the elastic constants) can be can be calculated in Console Mode for individual phases or all phases. The results can be shown in the POLY module with the command SHOW_VALUE or shown as a plot in the POST module with the command PLOT_DIAGRAM using:
Cij(<phase name>)orCij(*)- Bulk modulus:
BULKMOD(<phase name>)orBULKMOD(*) - Shear modulus:
SHEARMOD(<phase name>)orSHEARMOD(*) - Young's modulus:
YOUNGMOD(<phase name>)orYOUNGMOD(*)
For the Software Development Kits (SDKs), i.e. TC-Python and TC-Toolbox, the quantities of elastic constants, bulk modulus, shear modulus, and Young’s modulus can be retrieved for individual phases or all phases via get_value_of() or get_values_of() from any equilibrium calculation types using:
Cij(<phase name>)orCij(ALL_PHASES/*)ThermodynamicQuantity.bulk_modulus(<phase name>)orThermodynamicQuantity.bulk_modulus(ALL_PHASES/*)ThermodynamicQuantity.shear_modulus (<phase name>)orThermodynamicQuantity.shear_modulus(ALL_PHASES/*)ThermodynamicQuantity.youngs_modulus(<phase name>)orThermodynamicQuantity.youngs_modulus(ALL_PHASES/*)
See the relevant SDK documentation for details.
Units
When plotting or tabulating the elastic moduli in Graphical Mode you can choose between several units of pressure. The default unit for elastic moduli in the Plot Renderer and Table Renderer is GPa.
The elastic moduli and elastic constants are given in SI units, i.e. the values calculated in TC‑Python, TC‑Toolbox, and Console Mode are in Pascal.
Specific Database Use Case Examples
Each of the following databases have examples available to show how the elastic properties are applied within Thermo-Calc.
The TCS Ti/TiAl-based Alloys Database (TCTI) Validation and Calculation Examples Collection has examples using elastic properties. You can find a description of these either in the Thermo-Calc help
An example of the effect of oxygen concentration on Young’s modulus in HCP_A3 titanium is included with the Thermo-Calc installation. See T_19: Young's Modulus for Ti-O with Elastic Properties.
The TCS Steel and Fe-alloys Database (TCFE) Validation and Calculation Examples Collection has an example using elastic properties. You can find it either in the Thermo-Calc help
The TCS High Entropy Alloys Database (TCHEA) Validation and Calculation Examples Collection has an example using elastic properties. You can find it either in the Thermo-Calc help
The TCS Ni-based Superalloys Database (TCNI) Validation and Calculation Examples Collection has an example using elastic properties. You can find it either in the Thermo-Calc help
Reference
[2021Joh] E. Johansson, PhD thesis, Theoretical studies of the coupling between electronic, vibrational, configurational and structural effects in metal borides, Linköping University (2021).