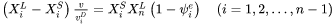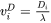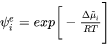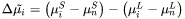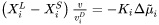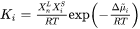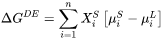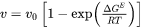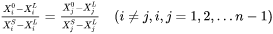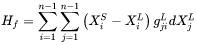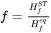About Scheil with Solute Trapping
The Scheil with solute trapping model simulates deviation from local equilibrium for the primary phase. It is useful for high solidification speeds, such as those seen in additive manufacturing applications.
For equilibrium- and classical Scheil-type solidification simulations thermodynamic equilibrium is established at the solid-liquid interface. This means that solutes are partitioned between the solid and liquid phases according to solidus and liquidus lines of the phase diagram. The assumption of thermodynamic equilibrium at the solid-liquid interface however, is invalid for very fast solidification rates, as encountered for example during additive manufacturing. The faster the solidification rate, the less the partitioning at the interface, which can be perceived as that solutes in the liquid are trapped in the advancing solid phase, hence the term solute trapping.
The Scheil with solute trapping model calculates the solute partitioning between liquid and primary solid that deviates from thermodynamic equilibrium due to solidification speed.
The following assumptions are made:
- Only one primary solid phase forms dendrite, NOT necessarily the first solid phase.
- Solute trapping in primary solid phase only. Other solid phases have equilibrium compositions following Scheil model.
- Dynamic liquidus for primary solid phases is dependent on solute trapping and solidification speed.
- Amounts of solid phases are dependent on solute trapping and solidification.
The model is based on Aziz [1982Azi; 1988Azi] and Hillert [1999Hil], and extends to multicomponent systems. The motion of liquid/solid interface is regarded as two concurrent processes, trans-interface diffusion (solute transport across the interface leading to solute partitioning) and migration (liquid to solid transformation without changing composition).
Aziz and Hillert used slightly different formulations to describe the trans-interface diffusion. Aziz [1982Azi; 1988Azi] formulated the expression in terms of chemical reaction theory, describing the diffusion of the 
th solute element (the dependent element being labeled as 
in a 
-component system) with respect to chemical potential gradient and interface velocity 
as:
Where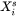 
and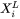 
are compositions (mole fractions) of primary solid and liquid at the interface, respectively. 
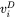is the diffusion velocity defined as:
Where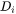 
is the trans-interface diffusivity and 
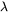is the interface thickness. In the software, 
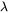is treated as a constant of 
m.
In Eq. 1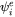 
is an activation term for diffusion:
Where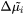 
is the diffusion potential difference:
Where 
and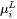 
are chemical potentials of 
th element in the primary solid and liquid at the interface.
Hillert [1999Hil], on the other hand, formulated the expression based on diffusion theory as:
Where:
For migration process, the formulation relates the free energy change, or driving force that is opposite to free energy change, to the interface velocity. The overall free energy change (termed as driving energy), including both trans-interface diffusion and migration processes, is defined as:
The free energy change for migration process (termed as migration energy) is:
The interface velocity is then related to the free energy change as:
Where:
-
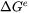can be either 
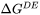or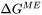 
defined in Eq. 7 and Eq. 8. -
is the maximum velocity limit when the free energy change becomes infinitely negative.
Additionally, the mass conservation within the interface is assumed:
Where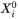 
is the far-field liquid composition.
Eq. 1 (for Aziz model) or Eq. 5 (for Hillert model), together with Eq. 9 and Eq. 10 are then used to calculate the solute partitioning at the interface between primary solid and liquid for multicomponent systems. Likewise, if replacing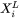 
with the initial alloying compositions, Eq. 1 (Eq. 5) and Eq. 9 are used to calculate the dynamic liquidus of the primary solid phase.
Solute trapping also reduces the volume fraction of other solid precipitates. The reduction factor is estimated by employing the effect of the solute trapping on the heat of fusion, which can be manifested by the liquid + primary solid phase boundaries in the phase diagrams by [1998Hil]:
Where all values are determined at phase boundaries.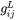 
is the second partial derivative of Gibbs free energy of liquid phase with respect to mole fraction. The left side of Eq. 11 is the enthalpy change when one (1) mole of primary solid with composition 
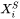is melted into a reservoir of liquid. Since we are interested in a ratio, the term that needs to be considered is:
The reduction factor is then obtained by comparing solute trapping with equilibrium values:
Scheil Calculator Configuration Settings
The Graphical Mode settings are described in Scheil Calculator: Configuration Window Settings.
T_13: Scheil Solidification with Solute Trapping
On the Configuration window, these are the relevant settings related to solute trapping:
- Trans-interface diffusivity (
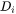): Smaller value leads to larger solute trapping effect. Be cautious that 
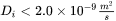may result in complete solute trapping and possibly numerical errors. - Maximum velocity for infinite driving force (
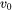): Smaller values lead to a larger solute trapping effect. - Choose the solute trapping Model (Aziz or Hillert): Hillert model usually leads to a larger solute trapping effect, though Aziz model is recommended for overall numerical performance including calculating the amount of non-primary solid phases.
- Interface driving force: Driving energy
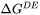or Migration energy
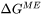. Using migration energy option leads to larger solute trapping effect, while using driving energy option is numerically more stable. It is recommended to using driving energy option and adjusting other parameters (e.g., trans-interface diffusivity) for desired solute trapping effect.
References
[1982Azi] M. J. Aziz, Model for solute redistribution during rapid solidification. J. Appl. Phys. 53, 1158–1168 (1982).
[1988Azi] M. J. Aziz, T. Kaplan, Continuous growth model for interface motion during alloy solidification. Acta Metall. 36, 2335–2347 (1988).
[1998Hil] M. Hillert, Phase Equilibria, Phase Diagrams and Phase Transformations: A Thermodynamic Basis (Cambridge University Press, 1998), 596 pp.
[1999Hil] M. Hillert, Solute drag, solute trapping and diffusional dissipation of Gibbs energy, Acta Mater., 47(18)4481-45-5(1999)