STEP_WITH_OPTIONS

When you accept the default, Normal (N), it allows a stepping calculation with the chosen independently-varying equilibrium condition (axis-variable). Only the step axis value is changed between each step.

When you repeat the STEP → NORMAL command-sequence, you can make several stepping calculations while still keep all the stepping-calculation results in the current POLY3 workspaces.

The calculation results are saved in the default RESULT.POLY3 file or you can specify to save it in the <MyName>.POLY3 file. This is as long as there is no SAVE_WORKSPACES command before the second set of command sequences (STEP → NORMAL). Repeated stepped results can be restored into the same current POLY3 workspaces/file.

Linux and Mac are case sensitive so ensure you enter .POLY3.

The addition of several steps enables you to generate special types of property diagrams and to calculate and plot special phase boundary lines on phase diagrams, such as:

• The missing part(s) of a specific property [that are calculated under another controlling condition inside the range of the stepping-variable] on the same property diagram.
• Two or more sets of a specific property [that are calculated under different controlling conditions and stepped over the same stepping-variable range] on the same property diagram for the same system.
• Calculate some special phase-boundary lines [especially for some defined secondary phase transformations or alike, e.g. the BCC_A1 <--> BCC_B2 phase-boundary, or equal-Gm for two specific phases, or equal-fraction or equal-activity for a certain species in two specific phases, that shall be calculated under different controlling-conditions and also be stepped over different stepping variable(s)], and then plot (or impose) them onto a corresponding phase diagram (which can be resulted from several such STEP → NORMAL calculations or  even from a separate MAP calculation) for the same system.

An initial equilibria is added at each calculated point. This can be useful, for instance, to generate a set of isothermal calculations.

When you choose I, an initial equilibrium is stored at each calculated equilibria. It is intended to generate a matrix of calculated initial equilibria, first stepped under a STEP INITIAL_EQUILIBRIA command-sequence and then repeated by another STEP NORMAL command-sequence (or even continued by a MAP command).

For example, you can first use the temperature condition as the stepping axis-variable with this option, which calculates a number of initial equilibrium points and automatically adds each one as an initial equilibria for another STEP → NORMAL command-sequence (or even for a MAP command). Before the second STEP command (i.e. the STEP → NORMAL command-sequence), you can chose a compositional condition as the new stepping axis-variable; then the STEP → NORMAL command-sequence uses those created starting equilibrium points (at different temperatures) and steps in such a new compositional variable. As a result, these two STEP commands together give a matrix of values.

In this way, you can calculate how the Gibbs energy for a number of phases varies for different compositions. This is particularly useful to calculate Gibbs energies for complex phases with miscibility gaps and for an ordered phase that is never disordered (e.g. SIMGMA-phase, G-phase, MU-phase, etc.).

This option is recommended for STEPPING heterogeneous systems with both ordered phases and the disordered pairs.

When you choose O, the stepping calculation is conducted individually for one phase at a time. That is, it is stepped over the whole stepping variable range, but the stepping is repeated for all the entered phases in the defined system. This is particularly useful to properly step in composition for an equilibrium heterogeneous system with both ordered phases and the disordered pairs. Thus, instead of calculating for the same composition for each of the phases at each composition step, it starts the stepping in each of the phases in the default most-stable compositions (the major constitutions).

For Scheil-Gulliver simulations it is recommended you use the SCHEIL module.

Evaluate E is an advanced option and is useful when additional conditions (instead of the stepping variable) require changing during a stepping calculation. It allows a stepping calculation in a single axis with simultaneous evaluation of one or more variables after each step. As variables can be used as conditions, it means that you can change the conditions during the stepping. After a successful EVALUATE calculation, you can go to the POST module to manually define and plot property diagrams.

The variables given are evaluated after each step, which may change other conditions. This can be useful to perform the Ordinary ScheilGulliver Approach (non-equilibrium transformations) for simulating alloy solidification without back diffusion of fast-diffusing interstitial components in solid phases. However, it is recommended you use the SCHEIL module.

Specify the prompt:

Variable name(s): <Variable name>

The names of the variables that shall be evaluated after each step must be typed here.

The miscibility gap test is automatically used during stepping (see ADVANCED_OPTIONS) if a phase has two or more composition sets.

The miscibility gap test means that you can start calculating from high temperatures in a steel where the MC carbide is not stable. During the calculation, the MC carbide first becomes metastable with a composition different from the metallic FCC phase and later also becomes stable.

See Console Mode example tcex30A.

For Scheil-Gulliver simulations it is recommended you use the SCHEIL module.

This is an advanced stepping calculation designed for the Extended Scheil-Gulliver Approach (partial-equilibrium transformations) to simulate alloy solidifications with back diffusion of one or more fast-diffusing interstitial components (such as C, N, O, S, etc.) in solid phases is performed. It also will consider BCC-->FCC phase transformation (practically for steels) along the alloy solidification process.

To ensure a successful stepping calculation of mixed Scheil-Gulliver simulation of solidification process of a defined alloy system with a certain initial overall composition, it is important to note the following:

• For solution phases with possibility of miscibility gap existence, you have appropriately added the necessary composition set(s);
• You have already set the temperature condition as the stepping SET_AXIS_VARIABLE command, with minimum and maximum temperature points as well as an appropriate s temperature step for the cooling process).
• There must be a composition condition for each of the back diffusion components (i.e. fast-diffusing interstitial components, such as C, N and/or other elements) that are already defined in terms of mole-fraction or mass-fraction, e.g. X(C) and W(N). Otherwise, a stepping calculation with this option can fail.
• An initial equilibrium in which the LIQUID mixture phase is the only stable must be calculated. This is why it is good to start with a relatively high temperature condition for the initial equilibrium calculation. It is always necessary to reject or suspend the GAS mixture phase (if it exists) before the C-E and STEP commands, to avoid its formation along with LIQUID.
• In cases where fast-diffusing interstitial components are specified as back diffusion components, you can choose to allow BCC>FCC phase transformation (practically for steels) during the alloy solidification process.

These are the prompts for this option:

Fast diffusing components: <Fast diffusion interstitial(s)>

Specify one or more interstitial component(s) as the back diffusion component(s).

• If there is only one fast-diffusing interstitial component (e.g. C or N), type its name;
• If there are two or more fast-diffusing interstitial components (e.g. C, N and S), always type the names on the same line at once (separated by an empty space in between, e.g. C N S);
• If there is no fast-diffusing interstitial component to be considered, type NONE to ignore back diffusion entirely, meaning a normal Scheil-Gulliver simulation is performed.

Such specified back diffusion interstitial component(s) must be appropriately defined according to the phase constitution definitions of some major alloy solution phases (e.g. FCC, BCC, HCP, etc.). These are located on the interstitial/vacancy sublattices in such alloy solution phases; otherwise, such a Scheil-Gulliver simulation may not make sense at all.

Allow BCC -> FCC ? /Y/:

By default the BCC-->FCC phase transformation is allowed. This is usually a typical phenomenon along the cooling processes of steels/Fe-alloys.

During the calculation the simulated solidification path, including the locally-equilibrated phase assemblage (region), captured temperature condition (T in K), remaining liquid phase (NL, mole fraction), overall formed solid phases (NS, mole fraction) and latent heat formation (NH, J/mol) along the cooling process are shown after the information on starting temperature point of the alloy solidification process, e.g.

Solidification starts at  1743.15 K

Phase Region from   1.744150E+03 for:      LIQUID

Phase Region from   1.742525E+03 for:

     LIQUID

     FCC_A1#1

       1742.5250          0.9960          0.0040         -1.1824

       1742.4000          0.9795          0.0205       -202.1585    . . . . . .

Phase Region from   1.733150E+03 for:

     LIQUID

     BCC_A2

     FCC_A1#1

       1733.1500          0.3294          0.6707      -8032.6240

       1733.0250          0.3237          0.6763      -8095.1490    . . . . . .

After a successful calculation, you can go to the POST module to manually define and plot property diagrams for the alloy solidification process according to the chosen Scheil-Gulliver model, or to impose existing relevant experimental information or other types of calculated solidification results [e.g. Scheil-Gulliver simulation with or without considering fast-diffusing interstitial component(s), full-equilibrium approach, or Diffusion Module (DICTRA)-type simulation with moving-boundary conditions] onto the same plotted property diagrams.  Normally, the solidus temperature (T in Celsius) is set as one of the axis variables (usually as Y-axis in most cases), while the other plotted quantity on the other axis can be the amount of overall formed solid alloy phases (NS in mole-fraction or BS in mass-fraction), the amount of remaining liquid phase (NL in mole-fraction or BL in mass fraction), the heat of latent along the solidification process (NH in J/mol or BH in J/gram), among many other properties in the solidified alloy phases or in the whole alloy system.

See Console Mode example 41.

This advanced option allows a stepping calculation of the so-called T0 (T-zero) line in a diffusionless transformation (where two specific partially-equilibrated phases have the same Gibbs energy) along a composition variable which has already set as the stepping variable with SET_AXIS_VARIABLE.

The temperature condition cannot be set as the stepping variable if you want to make a STEP T-ZERO calculation.

Prior to performing the step T0 command sequence, and to ensure a successful calculation of T0 line between two specific phases after an initial equilibrium calculation in the current system, it is sometimes recommended to make a single T0 point calculation using ADVANCED_OPTIONS → T-ZERO.

Specify these prompts:

Name of first phase:  <Phase A>

Name of second phase: <Phase B>

The names of the target phases, for which the Gibbs energies equal to each other at each point on the T0 line, must be entered.

During the calculation, the T0 values are shown after the corresponding scanned conditions (of the stepping composition variable), e.g.

Phase Region from   1.000000E-01 for:

     BCC_A2

     FCC_A1

   1.000000E-01         940.24

   9.250000E-02         941.20

   . . . . . .

   2.500000E-03         977.61

   7.500000E-09         979.34

Phase Region from   1.000000E-01 for:

     BCC_A2

     FCC_A1

   1.000000E-01         940.24

   1.075000E-01         939.62

   . . . . . .

   2.950000E-01        1084.87

   3.000000E-01        1080.99

After a successful calculation, you can go to the POST module to plot the T0 line against the stepping composition variable or another varying axis, or to impose the calculated T0 line onto a normal phase diagram [normally plotted as a T-X isopleth].

See Console Mode examples 42 and 43.

This is an advanced option. Select P to calculate the paraequilibrium state between two specific phases (the paraequilibrium lines). It allows a stepping calculation of paraequilibrium lines where the chemical potential for one or more interstitial components (that are considered as back diffusion elements, such as C and N) but not for the other (s) in two partially equilibrated phases are equal.

More than one interstitial component can be treated as fast-diffusion species (such as C, N, O, S, etc., as individual or combined) in a paraequilibrium stepping calculation.

The composition condition for the interstitial components cannot be set as the stepping variable if you want to make this calculation.

To ensure a successful stepping calculation of paraequilibrium states between two specific phases in a defined alloy system, it is important to first make a starting-point equilibrium calculation with an initial overall composition in the current system. However, it is unnecessary to obtain an equilibrium in which either one or both of the target phases is stable.

The initial overall composition must have a reasonable setting for the desired paraequilibrium calculation for the two target phases. This is especially true where there is more than one interstitial component to be considered in the paraequilibrium state, because different interstitial components (for example C and N combined) may have significant different behaviours as partitioning into different structured phases; otherwise, for one chosen interstitial component the initial overall composition is OK for the paraequilibrium calculation between the specified two phases, but for other chosen interstitial component(s) it might be impossible to calculate the paraequilibrium state.

Always check if the chosen phaseA and phaseB have the exact same definition of elements and if the chosen interstitial components are all in the vacancy sublattice sites of the two phases; otherwise the program cannot find the paraequilibrium state (as it is impossible to correctly calculate u-fractions).

Always have a comprehensive understanding of the normal phase diagram for the currently investigated system, so that you make the appropriate choice of the phase pair and staring bulk composition for the system.

Always set the status of the chosen interstitial components as SPECIAL using the command:

CHANGE_STATUS COMPONENT <interstitial component> = SPECIAL

By doing this, you get a clear picture on u-fractions of various substitutional and interstitial components, which are different from the overall composition in the system. The SPECIAL status means that specified component(s) are not included in summations for mole or mass fractions. Therefore, all the composition variables plotted from the paraequilibrium calculations are u-fraction related quantities.

Always make a single-point paraequilibrium calculation by the command-sequence of ADVANCED_OPTIONS → PARAEQUILIBRIUM, prior to performing this STEP → PARAEQUILIBRIUM command-sequence, although this might not be always necessary for some systems.

With this stepping calculation specify the following:

Name of first phase:  <Phase A>

Name of second phase: <Phase B>

The names of the two target phases A and B, between which the paraequilibrium states establish, must be typed at the above two prompts subsequently or on the same (first) line at once (separated by an empty space, e.g. FCC BCC, FCC#2 M23C6).

It is important to understand that this is the calculation of a paraequilibrium state between the two specified phases.

Particularly, there are these issues to consider:

1. Both chosen phases must have similar interstitial/vacancy sublattices where the fast-diffusion interstitial component(s) occupy.
2. The choice on the target phase pair must be reasonable for the defined system and specified initial overall composition.
3. Both target phases should have phase constitution definitions that cover all the defined substitutional and interstitial components of the current alloy system; or
4. It is impossible to calculate the paraequilibrium state between the target phase pairs with given interstitial component(s) in the currently defined system.

Fast diffusing component: /C/: <Interstitial component(s)>

Fast diffusing component: /None/: <Interstitial component(s)>

The name(s) of the fast-diffusing interstitial component(s) (C as the default single component) must be given either one by one at each of the above prompts subsequently or in a combination (separated by an empty space in between, e.g. C N S) at the same (first) prompt; otherwise, press <Enter> key to start the paraequilibrium line stepping-calculation.

Note the following:

Such specified fast-diffusing interstitial component(s) must be appropriately defined according to the phase constitution definitions of the two selected phases: These must be located on the interstitial/vacancy sublattices in both chosen phases.

If there is only one fast-diffusing component which is carbon, press <Enter> to accept the default value (C) at the first prompt; if the single fast-diffusing interstitial component is another element (e.g. N), appropriately type interstitial component the name at the first prompt;

If there are two or more fast-diffusing components (e.g. C and N), type their names at the above prompts subsequently or at the same (first) prompt (separated by an empty space, such as C N);

To finish the input of fast-diffusing elements, accept NONE at a repeated prompt;

If NONE or a non-existing component name is typed at the first prompt, it means no back diffusion is to be considered, and the para-equilibrium calculation is thus cancelled entirely.

During the STEP → PARAEQUILIBRIUM calculation procedure, the calculated paraequilibrium states include the:

• corresponding stepping conditions (e.g. temperature in K, or the stepping composition variable of the matrix component or of one of substitutional components) which has already set as the stepping variable by the SET_AXIS_VAR command);
• amounts of the phase A in mole number [i.e. NP(phaseA)];
• amounts of the phase B in mole number [i.e. NP(phaseB)];
• contents of the interstitial component(s) in the phase A expressed in u-fractions [i.e. u-f(phaseA,component(s))];
• contents of the interstitial component(s) in the phase B expressed in u-fractions [i.e. u-f(phaseB,component(s))];
• LNACR(component) value(s) for the interstitial(s).

After a successful STEP → PARAEQUILIBRIUM calculation, you can go to the POST module to plot a paraequilibrium phase diagram, or to impose the calculated paraequilibrium states onto a normal phase diagram [normally plotted as a T-X isopleth with one of the considered interstitial component(s) as the x-axis variable].

However, the stepping calculation procedure for the currently specified paraequilibrium states between the two specified phases may find difficulties at some steps due to some possible numerical problems (normally regarding to the u-fractions of the interstitial components under some composition ranges), or it may completely fails. In the latter case, it implies that the chosen target phase pair may be unreasonable for the defined alloy system or for the defined initial overall composition, or one or both phases may have inappropriate phase constitution definitions regarding the specified interstitial component(s) and substitutional components. Then, you must either modify the settings of initial overall composition or specify the reasonable target phase pair with an appropriate choice of the fast diffusion interstitials in the defined alloy system.

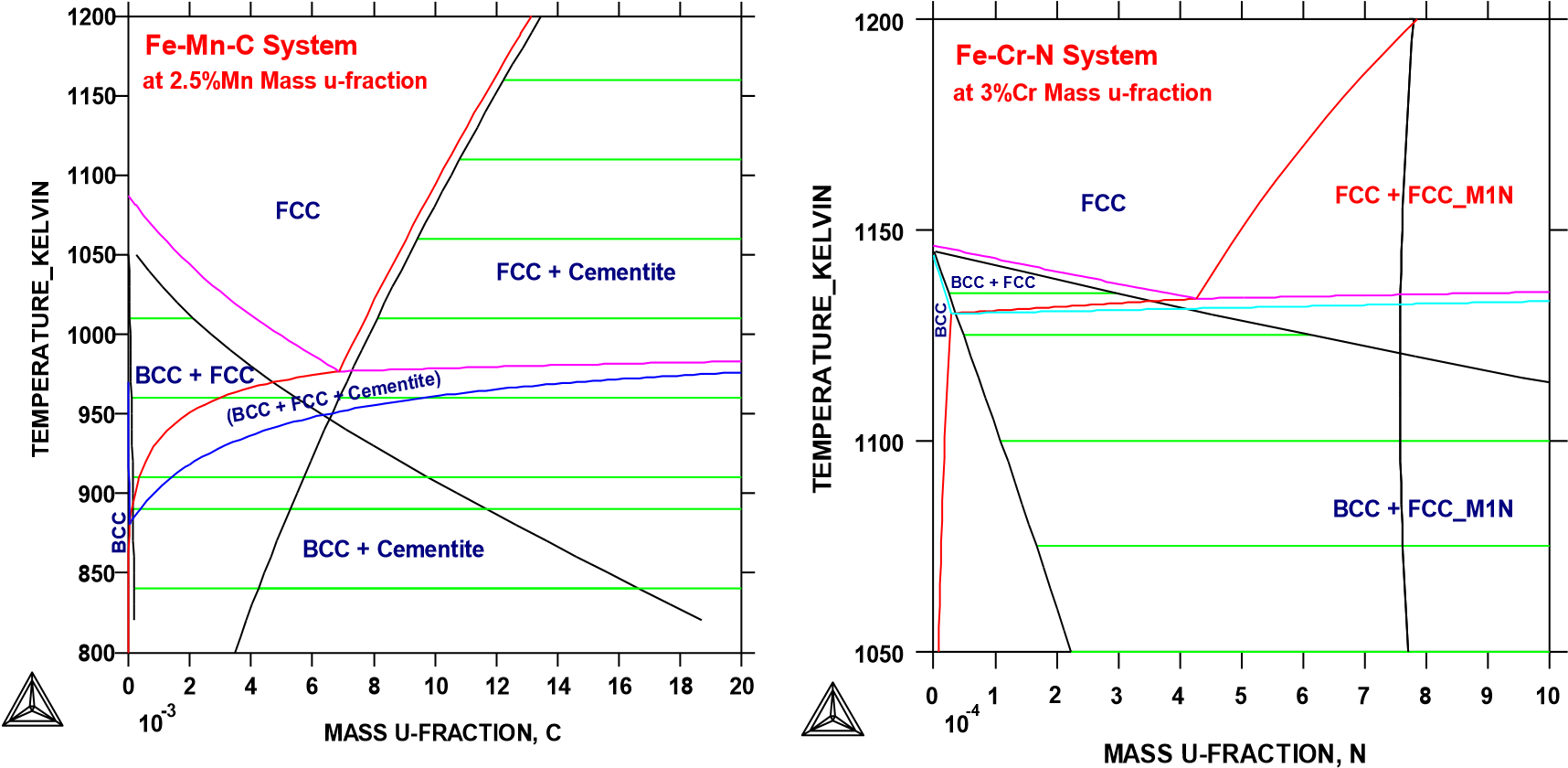
The figure shows the plot of a paraequilibrium calculation of isopleths: Formation of para-pearlite in two Fe-based alloys, with equilibrium results appended.

The calculated paraequilibrium phase boundaries (black lines) are shown with tie-lines (in green-colour). In the Fe-2.5Mn-C alloy system, C is considered as fast diffusing interstitial component in the BCC+FCC and FCC+Cementite paraequilibrium stepping calculations; while in the Fe-3Cr-N alloy system, N is treated as fast diffusing interstitial components in the BCC+FCC and FCC+FCC_M1N (i.e. FCC#1+FCC#2) paraequilibrium stepping calculations.

During a STEP calculation, the value of the stepping axis variable for each calculated equilibrium is listed and also the set of stable phases.

You can terminate the mapping of a line by pressing a single <Ctrl-A> (Windows) or <Ctrl-C> (Linux). This can be useful in order to stop a longish calculation without losing what is already calculated.

If there is any convergence problem in finding a stable solution at any stage during a calculation procedure enforced by a STEP_WITH_OPTIONS command-sequence, this message displays:

Convergence problems, increasing smallest site-fraction from 1.00E-30   to hardware precision 2.00E-14. You can restore using SET-NUMERICAL-LIMITS

This implies that smallest site fraction in the current POLY3 workspace is automatically increased from the default value 1.00E-30 to the hardware-dependent precision (under Linux, as 2.00E-14). For other subsequent POLY-module calculation in the current TC run, you can use the POLY command SET_NUMERICAL_LIMITS to restore or reset the smallest site fraction to the previous or another preferred value, as well as to reset other numerical limits.

Complex miscibility gaps of various solution phases are automatically detected during a stepping calculation, and two or more composition sets for each of such solution phases are automatically generated as well, through an automatic Global Minimization Test procedure (by specifying a Global Test Interval value and confirming the Automatically add initial equilibria in the ADVANCED_OPTION STEP_AND_MAP command-sequence). As a particular case, such an automatic Global Minimization Test ensures that you can now start calculating from high temperatures in an austenitic steel (metallic FCC_A1 solution phase) where the MC carbides/nitrides/carbonitrides (i.e. the C-/N-rich sides of the FCC_A1 miscibility-gap, often (while not always) being referred to as FCC_A1#2, FCC_A1#3, etc.) are not stable, and during the MAP command the MC carbides/nitrides/carbonitrides may first become metastable with a composition different from the metallic FCC_A1 phase and later also stable.

Occasionally, it may be necessary to have a specified increment other than the default value for the defined stepping axis-variable, in order to calculate/plot a smoother property diagram.

To get a complete property diagram, sometimes (especially in some earlier Thermo‑Calc versions) it may also be required to have more than one starting equilibrium-points (under another starting equilibrium condition), and repeat the stepping calculation over the same stepping axis-variable range (while without over-writing the same POLY3 workspaces via a SAVE_WORKSPACE command). However, using the current STEP procedure such a requirement become less necessary.