About the Columnar to Equiaxed Transition (CET) Property Model

The Columnar to Equiaxed Transition Property Model calculates the fraction of equiaxed grains that correlates with a certain solidification condition, specifically thermal gradient (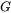) and solidification growth rate () (defined as the migration rate of the interface between liquid and primary solid), so that valuable information on the solidification microstructure can be obtained.

This General Model is available when using the Property Model Calculator in Thermo‑Calc. The Model formulation consists of two essential steps (1) to determine the dendrite tip radius and tip undercooling, and (2) to apply the calculated undercooling to the CET Model. These are discussed below.

Use of this Property Model requires mobility data of liquid for the calculations. For all simulations both a thermodynamic and a mobility (kinetic) database must be selected on the System Definer.

Determine the Dendrite Tip Radius and Tip Undercooling

The first step determines the dendrite tip radius and tip undercooling, which is strongly dependent on while slightly on 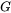. For this Model, only primary solid is assumed to be stable while other secondary solid phases are ignored. Mullins and Sekerka instability analysis [1964Mul] and marginal stability criterion [1978(a)Lan; 1978(b)Lan; 1978Mül] are used to determine the tip radius. Meanwhile, tip undercooling, 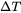, is also calculated due to constitutional, curvature, and solute trapping effects. The multicomponent extension of this framework is achieved based on the approach developed by Hunziker [2001Hun]. It integrates with both thermodynamic and mobility databases so that key thermodynamic and kinetic properties for multicomponent alloy systems, such as liquidus, liquidus slope, solute partitioning coefficients, and diffusivities of liquid, etc., can be obtained directly from the databases. Solute trapping effects on liquidus, liquidus slope, and solute partitioning are also considered based on the model developed by Aziz [1982Azi] and extended to multicomponent systems.

Apply the Undercooling to the CET Model

The second step is to apply the calculated undercooling, , to the CET Model. The model developed by Gäumann et al. [2001Gäu] is used, which extended Hunt’s model [1984Hun] to include high solidification rate. A slight modification [2018Hai] enables elimination of an adjustment parameter by directly using 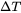. The model correlates , 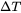(mostly in terms of ), and the fraction of equiaxed grain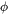s, , as

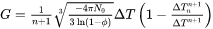
Where three materials related parameters are introduced:

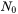• : number of nucleation sites per unit volume, in the unit of 1/m³
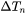• : nucleation undercooling, in the unit of K
• : exponent