About the Yield Strength Property Model
The Yield Strength Model is a general model to estimate the yield stress of a material that considers these contributions to the overall yield stress of the material:
- Intrinsic strength (
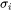) for the pure elements, - Grain boundary strengthening (
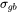), - Solid solution strengthening (
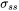), - Precipitation strengthening (
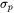), and - A user set, constant strength contribution (
).
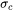The temperature (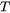
) is used to evaluate the equilibrium state of the system, and the resulting compositions and phase fractions are subsequently used in the evaluation of mechanical properties.
It returns the calculated yield strength at room temperature for the specified material using the equilibrium values calculated at temperature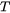 
(i.e. 
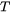is the freeze-in temperature).
Below follows a short summary for each of the contributions.
Intrinsic Strength
The intrinsic strength model formulation for this Property Model corresponds to a surface of reference with end-members. For example, for FCC_A1 modeled as (Fe,Ti)(C,Va), the intrinsic strength is a linear combination (as given by the composition) of Fe:Va (i.e. pure FCC Fe), Ti:Va (i.e. pure FCC Ti), Fe:C (i.e., FCC FeC) and Ti:C (i.e., FCC TiC). With such an implementation, it is possible to calculate yield strength for materials with a significant fraction of hard phases, such as carbides, embedded in a soft matrix and the intrinsic strengthening effect of interstitial elements.
The general form of the intrinsic strength model follows in the spirit of the Compound Energy Formalism (CEF) surface of reference term, where the intrinsic strength for, e.g., a two-sublattice phase model would correspond to:
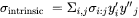
Such a formulation means that the intrinsic strength depends on the calculated site fractions from, e.g., an equilibrium calculation.
Phases with Assessed Intrinsic Strength
Not all compound phases are yet assessed in terms of intrinsic strength. The following phases are assessed: BCC_A2, CEMENTITE_D011, FCC_A1, FCC_L12, HCP_A3, M23C6_D84, M3C2_D510, M6C_E93, M7C3_D101, MC_SHP, MB2_C32, MOB2_C32, M3B2_D5A, M2B_CB, and MB_B33.
Temperature Dependence for Pure Elements
The following pure elements can be used to evaluate yield strength at non-room temperature conditions:
-
Ag, Al, Au, Be, Ce, Co, Cr, Cu, Dy, Er, Fe, Gd, Hf, Ho, Ir, La, Mg, Mo, Nb, Nd, Ni, Pd, Pt, Rh, Sm, Ta, Ti, U, V, W, Y, Zn, and Zr
The temperature dependence is of the form:
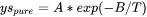
and is available for the listed pure elements where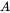 
and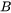 
are fitted to data from [1968Sam; 2017Wu]. This improves the results for evaluated yield strength at non-room temperature conditions.
The calculated solid solution strength can differ from versions of Thermo‑Calc prior to 2022b where the pure element strength from Cordero et al. was used [2016Cor]. This is especially noticeable for pure element or dilute solution calculations. The pure element strength is only evaluated for FCC, BCC, and HCP.
Compound end-members of the intrinsic model are not modeled as temperature dependent, however, this should have only a small effect on most alloys.
Constant Addition of Strength
The constant strength contribution parameter,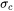 
, is set by the user as a constant strength addition to the material.
Grain Boundary Strengthening
The grain boundary strengthening,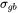 
, is the contribution to the total strength stemming from the grain boundary's ability to hinder dislocation movement described by the Hall-Petch relation [2004Han].
The parameters entered are the Hall-Petch constant,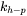 
, in MPa μm1/2, and the average grain diameter in μm.
Solid Solution Strengthening
The solution strengthening,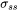 
, is the contribution to total strength due to the elastic strains in the crystal lattice caused by alloying elements of a lattice parameter differing from the main constituent. For the solid solution strengthening the option of evaluating the strength at any temperature is available. The result is normalized with respect to the sum of all mole fractions for FCC, BCC, and HCP. This option uses the phase fractions and compositions calculated at the overall equilibrium temperature. The model by Walbrühl et al. [2017Wal] is implemented.
PM_G_06: Yield Strength HEA shows how this model is applied.
Precipitation Strengthening
The precipitation strengthening, 
, is the contribution to total strength due to precipitation of a secondary phase, e.g. gamma prime (γ') in Ni-base alloys or Al3Sc precipitates in Al-base alloys. This model is available for any number of precipitating phases. The total particle strength is calculated by the square mean of the individual particle strength contributions:
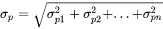
The Simplified model (general), Seidman model (Al-base), Reppich model (Ni-based), and Deschamps model (Al-base) are available as settings on the Configuration window to estimate the precipitation strengthening contribution. These are briefly described next.
Simplified Model (General)
The Simplified model (general) is based on the work by Zander et al. [2008Zan] and considers the general mechanisms of cutting and looping without regard to any detailed dislocation mechanisms. The default parameters are, however, optimized against experimental data for the Al-0.3wt%Sc alloy described by Seidman et al. [2002Sei]. Also see Mean Precipitate Radius and Particle Size Distribution (PSD) below.
PM_G_04: Yield Strength compares the Simplified model (general), Seidman model (Al-base), and Deschamps model (Al-base) yield strength versus precipitate radius to experimental data for an Al-0.3wt%Sc alloy homogenized at 648 °C for 24 hours and subsequently aged at 350 °C.
Seidman Model (Al-base)
The Seidman model (Al-base) by Seidman et al. [2002Sei] considers several contributions to the overall precipitation strengthening - ordering, coherency stresses, shear modulus mismatch, and Orowan looping. The Seidman model is suitable for Al-base alloys with a low volume fraction of spherical precipitates. Also see Mean Precipitate Radius and Particle Size Distribution (PSD) below.
PM_G_04: Yield Strength compares the Simplified model (general), Seidman model (Al-base), and Deschamps model (Al-base) yield strength versus precipitate radius to experimental data for an Al-0.3wt%Sc alloy homogenized at 648 °C for 24 hours and subsequently aged at 350 °C.
Reppich Model (Ni-base)
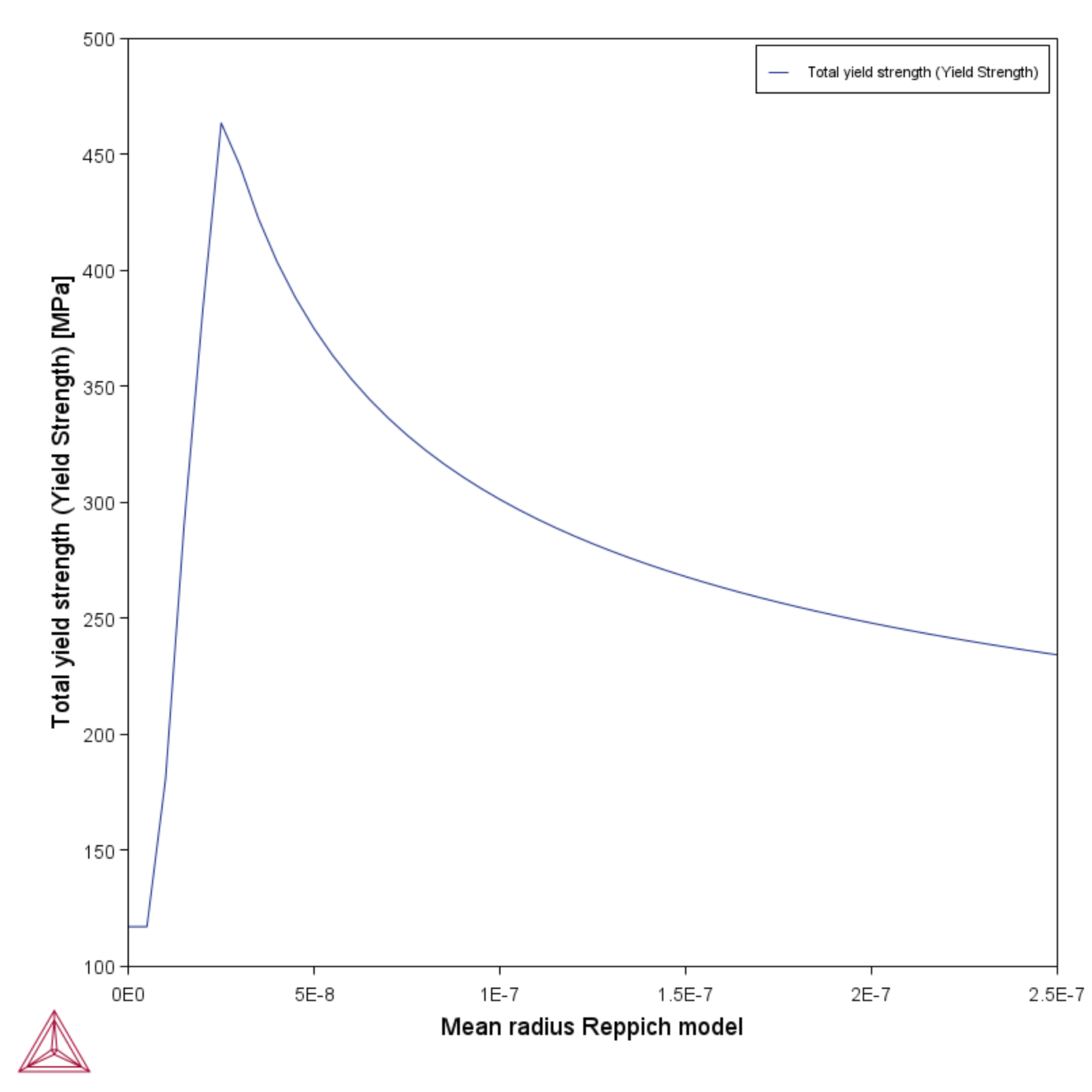
The Reppich model (Ni-base) by Reppich et al. [1982aRep] considers both weak and strong coupling of dislocation as they propagate through an ordered secondary phase and is thus suitable for Ni-base alloys with relatively high volume fractions of gamma prime or gamma double prime. Also see Mean Precipitate Radius and Particle Size Distribution (PSD) below.
The Reppich model is not valid for very small values of volume fraction precipitate and precipitate radius.
PM_G_05: Yield Strength NiAlCr is an example of this model.
![Reppich model plotted with results and experimental data for PE16 [6], all data is normalized with the square root of the volume fraction of precipitate.](../resources/images/propmodels/propmodysm_4.png "Reppich model plotted with results and experimental data for PE16 [6], all data is normalized with the square root of the volume fraction of precipitate.")
Figure 1: Reppich model plotted with results and experimental data for PE16 [1982bRep], all data is normalized with the square root of the volume fraction of precipitate.
Figure 2: Reppich model yield strength vs mean precipitate radius for Ni-10Cr-10Al.
Deschamps Model (Al-base)
The Deschamps model (Al-base) by Deschamps and Brechet [1998Des] considers contributions to the overall precipitation strengthening precipitate from particle cutting and Orowan looping. The Deschamps model is suitable for Al-base alloys with a low volume fraction of spherical precipitates. However, it has been successfully validated against other alloy types, such as Fe-based ferritic materials with TiC precipitates. Also see Mean Precipitate Radius and Particle Size Distribution (PSD) below.
The Deschamps model considers Friedel statistics as a default setting, with the option to instead apply Kock's statistics, as shown in the PM_G_04 example.
PM_G_04: Yield Strength compares the Simplified model (general), Seidman model (Al-base), and Deschamps model (Al-base) yield strength versus precipitate radius to experimental data for an Al-0.3wt%Sc alloy homogenized at 648 °C for 24 hours and subsequently aged at 350 °C.
Mean Precipitate Radius and Particle Size Distribution (PSD)
The mean precipitate radius entered on the Configuration window for all precipitation strengthening models is transformed to a Lifshitz-Slyozov-Wagner (LSW) particle size distribution [2010Tir]. The distribution is stepwise integrated and the mean radius for all sections are used to calculate a partial precipitate strengthening contribution. The partial contributions are added as
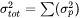
The use of a PSD smooths the transition between the cutting and Orowan regions. This change is implemented for the Simplified model (general) and Seidman model (Al-base).
When using the Yield Strength Model with the Precipitation Module (TC-PRISMA) the PSD as calculated by Precipitation Module (TC-PRISMA) is used for each time step. Also see Precipitation Calculator Plot Renderer for the settings input related to this.
Configuration Settings and References
Configuration Settings
The settings are entered on the Configuration window for the Property Model Calculator and described in Yield Strength Property Model: Simplified Mode Settings and Yield Strength Property Model: Advanced Mode Settings.
Yield strength is also available as a variable when working with Plots and Tables that are successors to the Precipitation Calculator.
References
[1968Sam] G. V. Samsonov, Handbook of the Physicochemical Properties of the Elements (Springer US, Boston, MA, 1968; 2012 American Edition).
[1982aRep] B. Reppich, Some new aspects concerning particle hardening mechanisms in γ’ precipitating Ni-base alloys—I. Theoretical concept. Acta Metall. 30, 87–94 (1982).
[1982bRep] B. Reppich, P. Schepp, G. Wehner, Some new aspects concerning particle hardening mechanisms in γ’ precipitating nickel-base alloys—II. Experiments. Acta Metall. 30, 95–104 (1982).
[1998Des] A. Deschamps, Y. Brechet, Influence of predeformation and ageing of an Al–Zn–Mg alloy—II. Modeling of precipitation kinetics and yield stress. Acta Mater. 47, 293–305 (1998).
[2002Sei] D. N. Seidman, E. A. Marquis, D. C. Dunand, Precipitation strengthening at ambient and elevated temperatures of heat-treatable Al(Sc) alloys. Acta Mater. 50, 4021–4035 (2002).
[2004Han] N. Hansen, Hall–Petch relation and boundary strengthening. Scr. Mater. 51, 801–806 (2004).
[2008Zan] J. Zander, R. Sandström, One parameter model for strength properties of hardenable aluminium alloys. Mater. Des. 29, 1540–1548 (2008).
[2010Tir] M. Tiryakioğlu, G. Ökten, D. Hudak, R. T. Shuey, J. P. Suni, On evaluating fit of the Lifshitz–Slyozov–Wagner (LSW) distribution to particle size data. Mater. Sci. Eng. A. 527, 1636–1639 (2010).
[2016Cor] Z. C. Cordero, B. E. Knight, C. A. Schuh, Six decades of the Hall–Petch effect – a survey of grain-size strengthening studies on pure metals. Int. Mater. Rev. 61, 495–512 (2016).
[2017Wal] M. Walbruhl, D. Linder, J. Ågren, A. Borgenstam, Modelling of solid solution strengthening in multicomponent alloys. Mater. Sci. Eng. A. 700, 301–311 (2017).
[2017Wu] Z. Wu, M. C. Troparevsky, Y. F. Gao, J. R. Morris, G. M. Stocks, H. Bei, Phase stability, physical properties and strengthening mechanisms of concentrated solid solution alloys. Curr. Opin. Solid State Mater. Sci. 21, 267–284 (2017).