EQUILIBRIUM_CALCUL

This is an option that is available with the ADVANCED_OPTIONS command with the POLY and ED-EXP modules.

Use this command to decide how to perform the POLY minimization (i.e. the traditional Gibbs energy minimization). The Global Minimization Technique is used by default for various single point equilibrium calculations and for stepping or mapping calculations.

To permanently turn off the Global Minimization Technique (for all sequential calculations throughout the current run), use the GLOBAL_MINIMIZATION command and set the options to use only the local POLY minimization. You can also make other adjustments to control the steps in reaching Gibbs energy minima in an equilibrium state, for example.

When enforcing the Global Minimization Technique in the equilibrium calculations, you can further adjust how to assign grid points and to handle compositional set(s) for solution phases during stepping/mapping. In order to improve convergence, and because the Global Minimization Technique uses the normal POLY optimization routine for some calculations, you can also change how to control the steps in reaching Gibbs energy minima in an equilibrium state.

Settings for the Minimization of an Equilibria

The following prompts show how the POLY optimization does the local POLY minimization to reach the minimum of an equilibrium state.

Force positive definite phase Hessian /Y/:

Choose Y or N to determine how to reach the minimum of an equilibrium state in a normal POLY optimization procedure. This is related to the special quantity, the phase stability function QF (phase), for all kinds of phases in an equilibrium state [a phase stability function for a phase is negative when the phase composition is inside a spinodal, and positive everywhere else].

If the composition of a solution phase is inside its spinodal, the enforcement of positive definite eigenvalues of a Hessian matrix (i.e. when Y is selected) makes the step be taken towards the minima rather than the local maxima. Furthermore, if an eigenvalue (for a phase) of the Hessian matrix is near 0.0, the step size is large this sets a lower limit to this eigenvalue, reducing the step-size and improving the convergence.

The POLY command sequence SHOW_VALUE QF(phase) shows the size of the lowest eigenvalue of a phase in an equilibrium state.

If you answer:

Y , it helps the local POLY minimization to converge (if there is a problem), especially if QF(phase)=0 for phases.
N the local POLY minimization routine is applied.

For each phase in a defined system, the molar Gibbs energy of the phase is a function of the temperature-pressure condition and its composition:

The molar Gibbs energy of the phase is a function of the temperature-pressure condition and its composition:

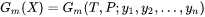
Compute a Hessian matrix, which describes the curvature of the Gibbs energy curve of this phase at the defined composition X:

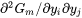
Diagonalize this matrix and call the Eigenvalues as e1,e2,...,en . The QF(phase) quantity for this phase is the lowest of these eigenvalues divided by the same values for a corresponding ideal phase:

The QF(phase) quantity for this phase is the lowest of these eigenvalues divided by the same values for a corresponding ideal phase:

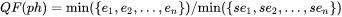
Here, se1,se2,...,sen are the Eigenvalues for the ideal phase. Therefore, for an ideal phase, the QF(phase) should always be 1.0.

Control stepsize during minimization /Y/:

Choose Y or N to determine whether to introduce a control of step size while reaching the minimum of an equilibrium state in a normal POLY optimization procedure. If you choose Y it might help the POLY optimization to converge, especially if some site fractions are less than 1E-4.