Yield Strength Property Model: Advanced Mode Settings
This section has information about the Advanced mode configuration settings available for the Yield Strength Property Model.
The Yield Strength Model is available with the Property Model Calculator and calculates yield stress.
Yield strength is also available as a quantity when working with Plots and Tables that are successors to the
The Yield Strength Model returns the calculated yield strength at room temperature (per default) for the specified material using the equilibrium values calculated at temperature 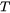 (i.e.
(i.e.  is the freeze-in temperature). The Model is defined by further setting these contributions:
is the freeze-in temperature). The Model is defined by further setting these contributions:
- Intrinsic strength (
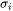 )
) - Solid solution strengthening (
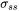 )
) - Grain boundary strengthening (
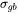 )
) - Precipitation strengthening (
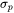 )
) - Constant strength addition (
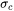 )
)
These contributions are defined in About the Yield Strength Property Model.
For examples using the Property Model Calculator, see PM_G_04: Yield Strength, PM_G_05: Yield Strength NiAlCr, and PM_G_06: Yield Strength HEA.
For an example when it is available as an axis variable with the Precipitation Calculator, see P_01: Isothermal Precipitation of Al3Sc.
General Configuration Settings
The settings for these contributions are found on the Property Model Calculator when the Yield Strength Model is selected under General Models.
For the details about the Condition Definitions, Calculation Type, Timeout in minutes, Parallel Calculation, and other calculation associated settings, see Property Model Calculator: Configuration Window Settings.
There are settings described elsewhere when Yield Strength is selected as an axis variable for a Plot Renderer or Table Renderer that are successors to the
When working in the Configuration window, click the Description tab for more information about the Model.
Advanced Mode Settings
Select Advanced as the Mode. Available settings are displayed based on the choice.
For the specific Simplified settings, go to Yield Strength Property Model: Simplified Mode Settings.
Select the Set matrix phase explicitly checkbox and choose a Matrix phase from the list. This allows forcing a specific phase to be considered as the matrix phase.
This is an important parameter as it impacts the evaluation of the shear modulus and affects the result for the precipitation strengthening contribution.
The solid solution strengthening contribution is not affected by choice of matrix phase, since all stable FCC, BCC, and HCP phases always are evaluated for solid solution strength contributions. If this option is not selected, the matrix phase is automatically determined by the model.
Select the Solid solution strengthening checkbox to include solid solution strengthening in the calculation.
This checkbox is available when the Solid solution strengthening checkbox is selected. By default the checkbox is not and the simulation is evaluated at room temperature.
Select the Evaluate at higher temperature checkbox to evaluate the contribution 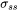 at temperatures higher than room temperature.
at temperatures higher than room temperature.
When selected, enter a Solid solution strengthening temperature in the field in numeric format (no expressions/functions are accepted). The unit of temperature is the same as that selected above under Condition Definitions.
If no temperature is entered, the default, room temperature, is used.
Click to select the Grain boundary strengthening checkbox to include calculated grain boundary strengthening (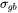 ). Then enter the Grain size [um], which is the grain diameter in micrometers (μm).
). Then enter the Grain size [um], which is the grain diameter in micrometers (μm).
By default, a suitable default Hall-Petch coefficient is automatically calculated by the model. Select the User defined Hall-Petch coefficient checkbox to enter a different Hall-Petch coefficient: 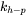 in MPa μm1/2.
in MPa μm1/2.
Click to select the Precipitation strengthening checkbox to include calculated precipitation strengthening (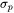 ). Then enter the settings that follow under the Precipitation Strengthening Model section.
). Then enter the settings that follow under the Precipitation Strengthening Model section.
The Precipitate list defaults to Any phase.
- If Any phase is selected as a Precipitate phase, the non-matrix-like phase with the highest volume fraction is selected. If more than one precipitate is defined and set to Any phase, non-matrix-like phases are selected in order of descending volume fraction.
- If more precipitates with Any phase are defined than there are stable non-matrix-like phases in the system, the redundant precipitates are ignored.
- Graphite is prohibited to be set as a precipitate phase.
Otherwise, select another phase from the list. Click the  and
and  buttons to add and remove additional Precipitates that can have different settings.
buttons to add and remove additional Precipitates that can have different settings.
The precipitation strengthening contribution (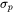 ) is calculated by one of these models, which are further described below.
) is calculated by one of these models, which are further described below.
Select a Precipitation strengthening model from the list:
- Simplified model (general)
- Seidman model (Al-base): Preferentially used for Al-based alloys.
- Reppich model (Ni-base): Preferentially used for Ni-based alloys.
The Reppich model is not valid for very small values of volume fraction precipitate and precipitate radius.
-
Deschamps model (Al-base): Preferentially used for Al-based alloys.
For the Simplified model (general), enter values in the fields for the following. The default values of 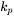 and
and 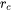 are optimized against experiments for Al-Sc.
are optimized against experiments for Al-Sc.
- Mean radius Simplified model: The precipitate mean radius. The unit is meter (m). Also see Mean Precipitate Radius and Particle Size Distribution (PSD)
- Critical radius (
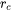 ), which determines the mean precipitate radius where transition between cutting and looping occurs. The unit is meter (m).
), which determines the mean precipitate radius where transition between cutting and looping occurs. The unit is meter (m). - kp: The prefactor for the Simplified model, which adjusts the overall height of the yield precipitation strength curve.
For the Seidman model (Al-base), enter values in the fields for the following. The default parameters are optimized against experiments.
- Mean radius Seidman model: The precipitate mean radius. The unit is meter (m). Also see Mean Precipitate Radius and Particle Size Distribution (PSD)
- Anti-phase boundary energy:
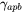 , which is the average anti-phase boundary energy for the precipitate phase. The unit is Jm-2.
, which is the average anti-phase boundary energy for the precipitate phase. The unit is Jm-2. - m: A Seidman exponent, it is a constant in the expression for strengthening by modulus mismatch. See [1985Ard] for details.
-
 : A Seidman prefactor. It is a fitting constant in the expression for coherency strengthening. See [1985Ard] for details.
: A Seidman prefactor. It is a fitting constant in the expression for coherency strengthening. See [1985Ard] for details.
For the Reppich model (Ni-base), enter values in the fields for the following. The default parameters are optimized against experiments.
- Mean radius Reppich model: The precipitate mean radius. The unit is meter (m).
- Anti-phase boundary energy:
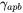 , which is the average anti-phase boundary energy for an L12 ordered precipitate phase. The unit is Jm-2.
, which is the average anti-phase boundary energy for an L12 ordered precipitate phase. The unit is Jm-2. - Calculate anti-phase boundary energy: Select the checkbox to use calculated anti-phase boundary energy in the yield strength calculation. The software uses the standalone APBE model in the Ni-library from within the Yield Strength Model for the calculation.
The APBE can only be calculated for gamma prime (γ'). If the selected precipitate phase is not γ', the user-defined value in the configuration window is used.
- w: A parameter that accounts for elastic repulsion between strongly coupled dislocations.
- A: Numerical factor reflecting particle morphology (0.72 for spherical). See [1982Rep] for details.
- C: Correction factor in the Labusch hardening regime, i.e. for gamma prime hardended Ni-base alloys. Should be larger than or equal to unity. Set to
0in order to disable correction.
For the Dechamps model (Al-base) enter values in the fields for the following. The default parameters are optimized against experiments.
- Mean radius Dechamps model: Precipitate mean radius. The unit is meter (m).
- Critical radius (
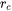 ), which determines the mean precipitate radius where transition between cutting and looping occurs. The unit is meter (m).
), which determines the mean precipitate radius where transition between cutting and looping occurs. The unit is meter (m). -
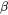 : A parameter used to evaluate the dislocation line tension. Usually close to 1/2 but can deviate from this value.
: A parameter used to evaluate the dislocation line tension. Usually close to 1/2 but can deviate from this value. - Use Kock's statistics: By default, Friedel statistics are used. Select the checkbox to use Kock's statistics instead. See [1998Des].
Additional Precipitation Parameters (Advanced Mode)
The following are available for all models and when the Additional precipitation parameters checkbox is selected.
Enter a value for the Taylor factor.
The value of the Taylor factor accounts for texture in the material. Normally the value is between 2.24 and 3.06 for random orientations.
Enter a value for the Shear modulus of the matrix phase in Pa.
Enter a value for the Burgers vector. The unit is meter (m).
Select the Constant strength addition checkbox and enter a value for the Constant strength addition, 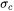 . The unit is MPa This accounts for any contributions not accounted for in the Yield Strength model, e.g. martensite strengthening.
. The unit is MPa This accounts for any contributions not accounted for in the Yield Strength model, e.g. martensite strengthening.
Select an Equilibrium minimization strategy. The default uses the Global test preferred option.
The Minimization Strategy setting is used to ensure that the most stable minimum under the specified conditions is computed.
With either the Global test preferred or Local minimization preferred setting, the program cycles through options before it gives up:
- For Global test preferred the minimization starts with a global test and if that fails it runs full global minimization.
- For Local minimization preferred the minimization starts with a local minimization, in case of failure it tries a global test and finally a full global minimization.
If you choose Local minimization only or Global minimization only, the program just tries the one setting and gives up if it fails.
For general information about global minimization, see the topic related to the Console Mode command, GLOBAL_MINIMIZATION.
This setting is only available for a precipitation calculation using the Precipitation Module (TC-PRISMA).
Select the Density of points: Low (the default), Medium, or High. This is a measure of how many time steps yield strength is calculated.
References
[1982Rep] B. Reppich, Some new aspects concerning particle hardening mechanisms in γ’ precipitating Ni-base alloys—I. Theoretical concept. Acta Metall. 30, 87–94 (1982).
[1998Des] A. Deschamps, Y. Brechet, Influence of predeformation and ageing of an Al–Zn–Mg alloy—II. Modeling of precipitation kinetics and yield stress. Acta Mater. 47, 293–305 (1998).