PM_G_04: Yield Strength

The example uses the Property Model Calculator and the Yield strength Property Model with a thermodynamic demonstration aluminum database (ALDEMO).

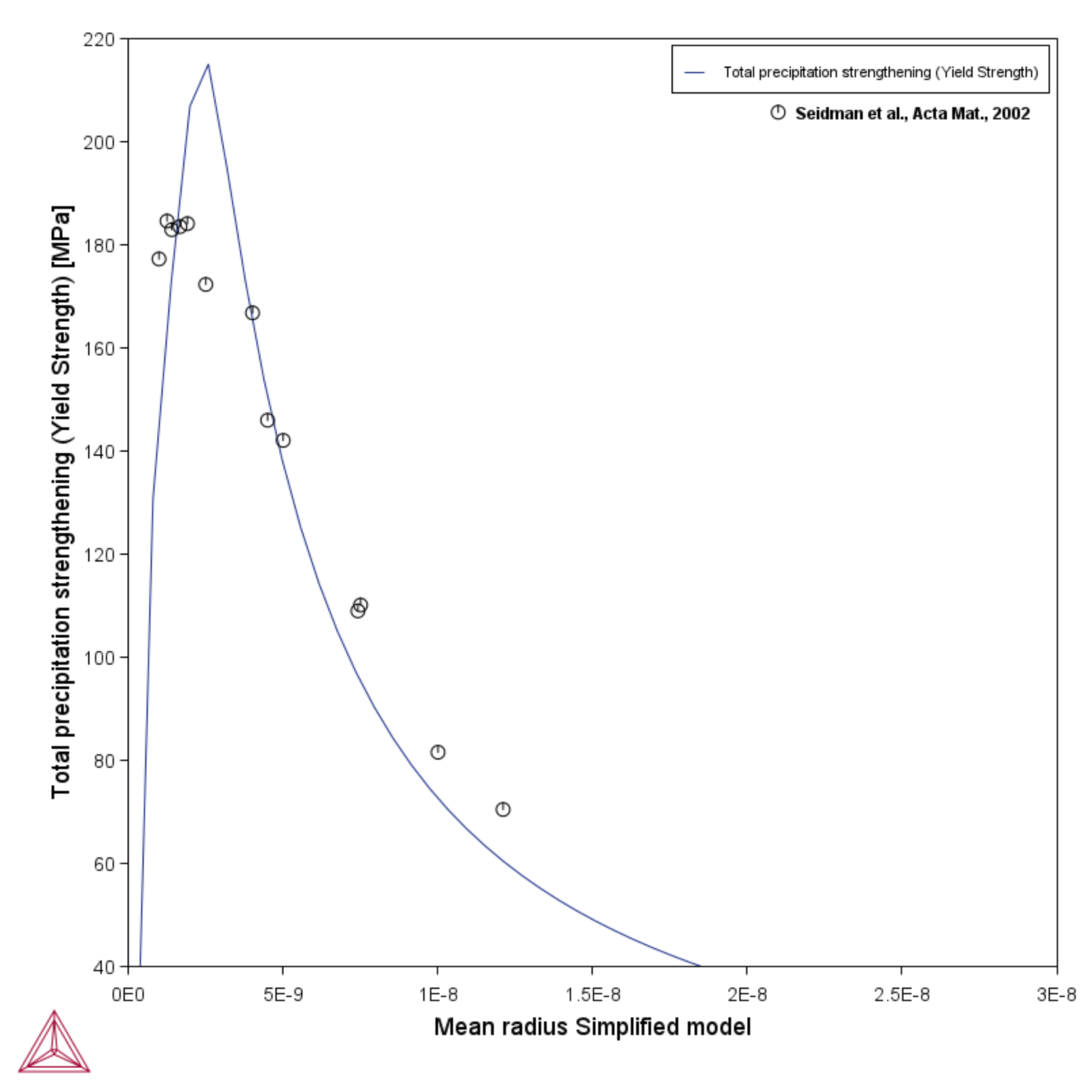
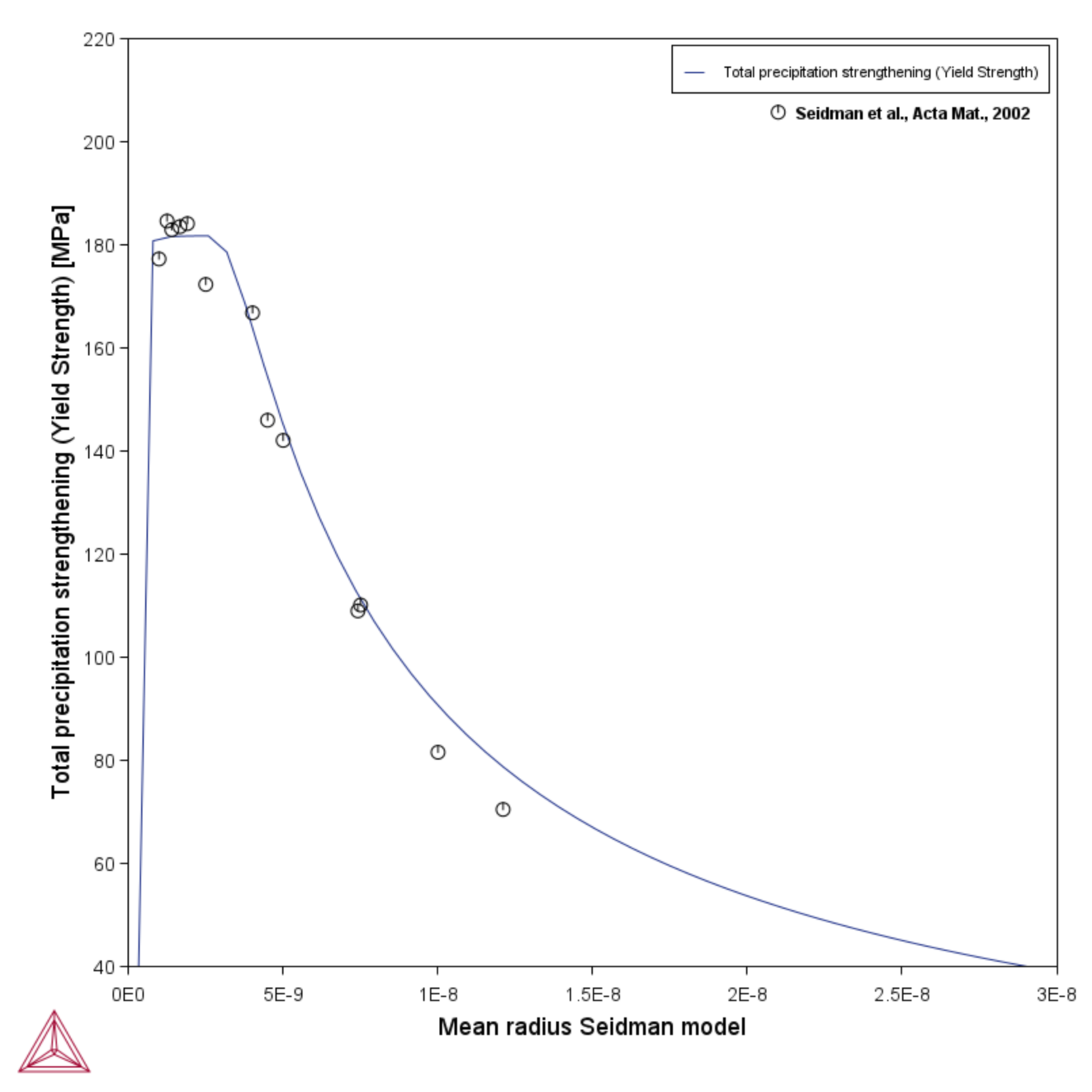
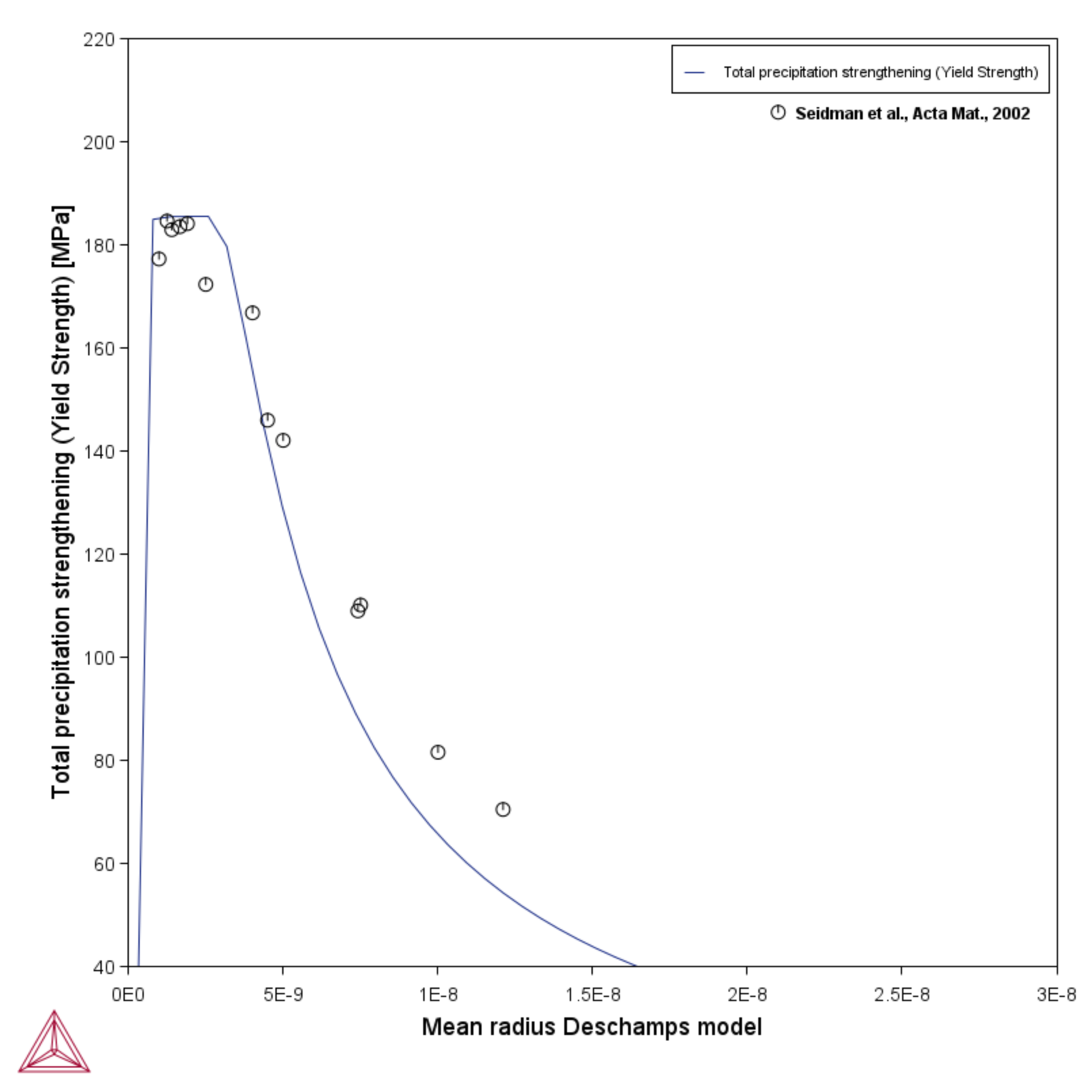
Using default options for the precipitation strengthening models, this example compares the Simplified model (general), Seidman model (Al-base) and Deschamps model (Al-base) yield strength versus precipitate radius to experimental data for an Al-0.3wt%Sc alloy homogenized at 648 °C for 24 hours and subsequently aged at 350 °C.

For more settings information, see Yield Strength Property Model: Simplified Mode Settings or Yield Strength Property Model: Advanced Mode Settings. For additional theoretical information about the models, see About the Yield Strength Property Model.

The Seidman model [2002Sei] considers a combination of a shearing mechanism and Orowan dislocation bypass mechanism. For the shearing mechanism, the increase in yield strength results from the contributions of ordering strengthening, coherency strengthening, and modulus mismatch strengthening.

When Seidman model (Al-base) is selected as the Precipitation strengthening model, the setting for prefactor for coherency stress contribution is a constant related to the coherency strengthening of precipitates, which usually varies from 2 to 3. In this example, the default prefactor for coherency stress contribution is 2.6 [1985Ard]. The m setting is the parameter that relates to the modulus mismatch strengthening and the default is set as 0.85 [1985Ard]. This model is applied in the study of precipitation hardening in dilute Al(Sc) alloys containing coherent Al3Sc precipitates. The model parameters described above can be adjusted to work for hardenable aluminum alloy calculations from the 2000 (Al–Cu and Al–Cu–Mg), 6000 (Al–Mg–Si), and 7000 (Al–Zn–Mg) series.

As a comparison, the Simplified model [2008Zan] only considers the general mechanisms of cutting and looping (Orowan mechanism) without regard to any detailed dislocation mechanisms.

When Simplified model (general) is selected as the Precipitation strengthening model, the default Critical radius (the critical size 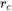Critical radius) is optimized against experimental results for dilute Al-Sc. If the precipitates are smaller than a critical size (approximately 5–10 nm) the dislocations cut the precipitates. The strength of the obstacle is then proportional to the square root of the average radius. If the particles are larger than the critical size, 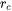Critical radius, it is less costly for the dislocations to bow round the particles and the strengthening contribution is inversely proportional to radius. Since the Simplified model (general) only depends on generic material constants (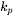prefactor for the simplified model and Critical radius) it may be applied to any precipitation strengthened material.

The Deschamps model (Al-base) model [1998Des], is for precipitation strengthening, mainly intended for use with Al-base alloys. The Deschamps model includes use of Friedel or Kock's statistics for particle size distribution. Default parameters are used to match a dilute Al-Sc alloy with Al3Sc precipitates. As is done for the other precipitation strengthening models, a critical radius, describing the transition from cutting to looping, must be specified when you are setting up the configuration.

  • Folder: Property Models → General
  • File name: PM_G_04_Yield_Strength.tcu

Visualizations

Many of our Graphical Mode examples have video tutorials, which you can access in a variety of ways. When in Thermo‑Calc, from the menu select Help → Video Tutorials, or from the main My Project window, click Video Tutorials. Alternately, you can go to the website or our YouTube channel.

Open the example project file to review the node setup on the Project window and the associated settings on the Configuration window for each node. For some types of projects, you can also adjust settings on the Plot Renderer Configuration window to preview results before performing the simulation. Click Perform Tree to generate plots and tables to see the results on the Visualizations window.

Strength vs Radius - Simplified compared to experimental data

Figure 1: Strength vs Radius - Simplified compared to experimental data from [2002Sei].

PM_G_04 Plot: Strength vs Radius (Seidman)

Figure 2: Strength vs Radius - Seidman compared to experimental data from [2002Sei].

Strength vs Radius - deChamps compared to experimental data

Figure 3: Strength vs Radius - Deschamps compared to experimental data from [2002Sei].

References

[1985Ard] A. J. Ardell, Precipitation hardening. Metall. Trans. A. 16, 2131–2165 (1985).

[1998Des] A. Deschamps, Y. Brechet, Influence of predeformation and ageing of an Al–Zn–Mg alloy—II. Modeling of precipitation kinetics and yield stress. Acta Mater. 47, 293–305 (1998).

[2002Sei] D. N. Seidman, E. A. Marquis, D. C. Dunand, Precipitation strengthening at ambient and elevated temperatures of heat-treatable Al(Sc) alloys. Acta Mater. 50, 4021–4035 (2002).

[2008Zan] J. Zander, R. Sandström, One parameter model for strength properties of hardenable aluminium alloys. Mater. Des. 29, 1540–1548 (2008).