TC‑Python Precipitation Examples
You do not need a Precipitation Module (TC-PRISMA) license to use these examples, which use up to three components and this is available for all users with a Thermo-Calc license.
To run more complex precipitation calculations, you need a Precipitation Module license.
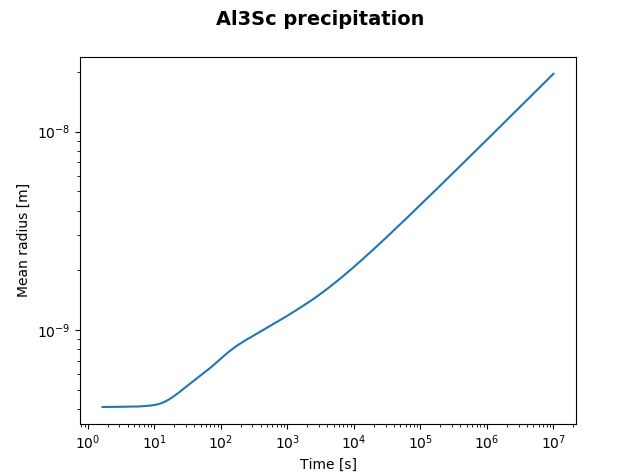
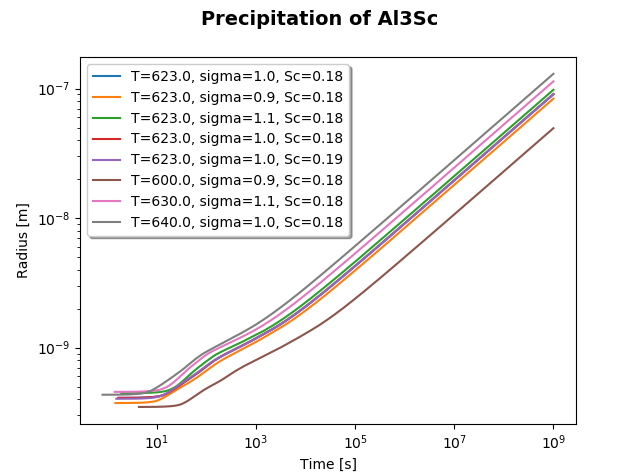
File name: pyex_P_01_Precipitation_Al-Sc_AL3SC.py
This example simulates the kinetics of precipitation of Al3Sc from an FCC_A1 solution phase and shows some results, with minimally required settings. Default values are used for unspecified settings.
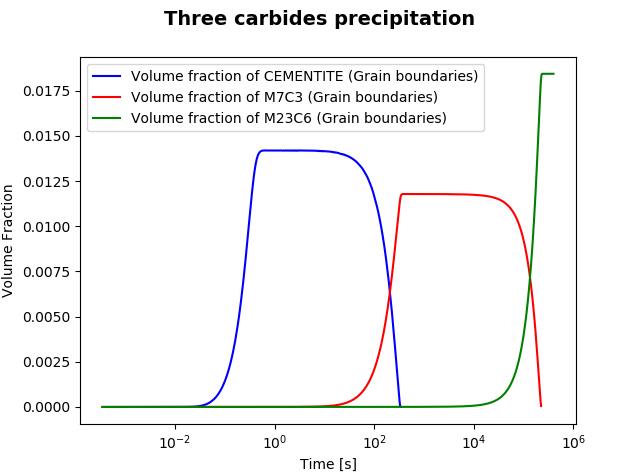
File name: pyex_P_02_Precipitation_Fe-C-Cr_Cementite-M7C3-M23C6.py
Also see the Graphical Mode example that this is based on: P_02: Stable and Metastable Carbides - Isothermal
This example simulates the kinetics of precipitation of both stable and metastable carbides from the ferrite phase. It demonstrates that metastable carbides (cementite, M7C3) may first emerge and then disappear and the stable phase (M23C6) prevails.
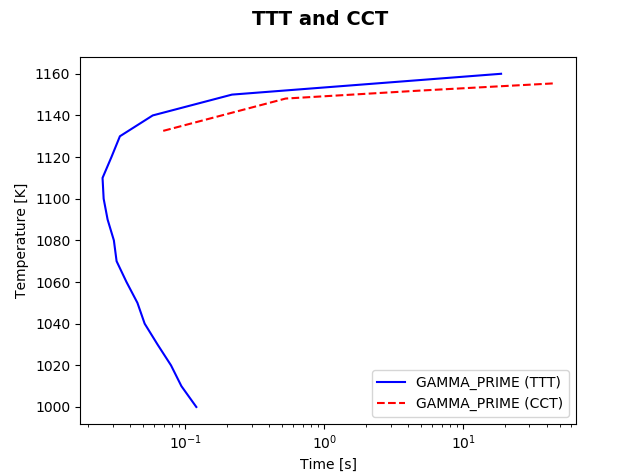
File name: pyex_P_03_Precipitation_Ni-Al-Cr_TTT_CCT_Gamma-Gamma_prime.py
This example simulates the precipitation of gamma-prime phase from gamma phase in a Ni-Al-Cr alloy. It demonstrates how to run TTT (temperature-time-transformation) and CCT (continuous-cooling-transformation) diagrams. It also shows (1) how to set up objects (the system, precipitate phase, and matrix phase) and then reuse them, and (2) how to set an alias for the precipitate phase.
This example takes several minutes to calculate. The results are updated continually. The plot examples shown are the final iterations.
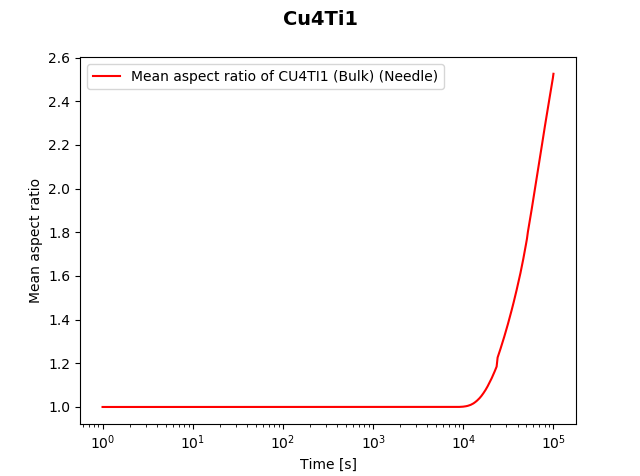
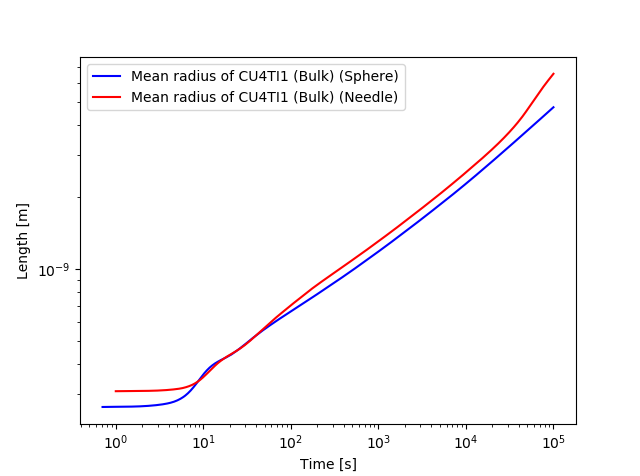
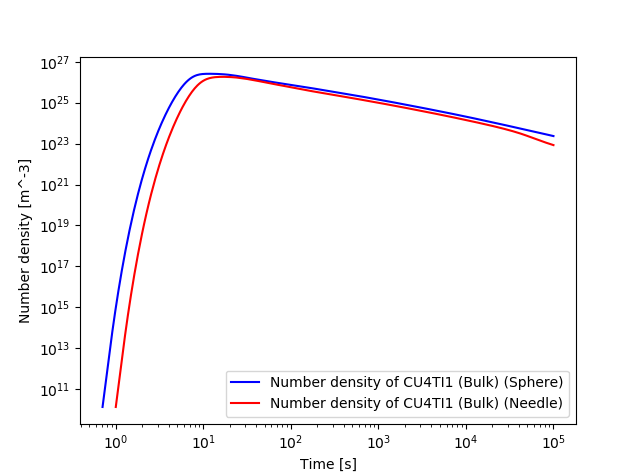
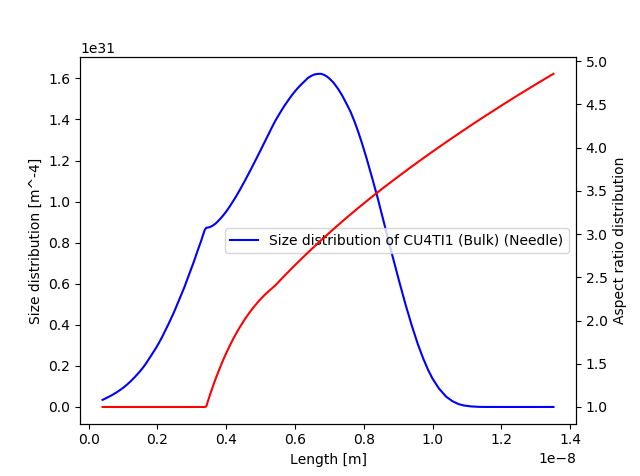
File name: pyex_P_04_Precipitation_Cu-Ti_CU4TI1_Sphere_Needle.py
Also see the Graphical Mode example that this is based on: P_08: Precipitation of Cu-Ti CU4TI with Assumptions of Sphere and Needle Morphologies
In this isothermal calculation example, the precipitation of the Cu4Ti phase in a Cu-Ti binary alloy is calculated. To make a comparison, two separate simulations are performed: (1) one assuming spherical morphology without elastic strain energy, and (2) one assuming needle morphology whose shape, determined by competition between interfacial energy and elastic strain energy, is changed during the simulation.
This example takes several minutes to calculate. The results are updated continually. The plot examples shown are the final iterations.
File name: pyex_P_05_Precipitation_Al-Sc_AL3SC_Multiprocess.py
This example shows how to set up multiple precipitation calculations with different parameter settings and send them to four processors for concurrent execution.
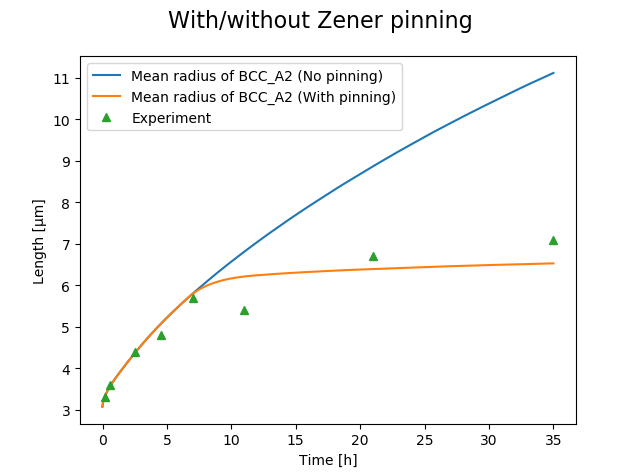
File name: pyex_P_06_Precipitation_Fe_C_zenner_pinning.py
Also see the Graphical Mode example that this is based on: P_14: Grain Growth and the Zener Pinning Effect
This example simulates the kinetics of precipitation of CEMENTITE from a BCC_A2 solution phase and shows the grain growth results for two cases: with and without Zener pinning. A log normal distribution is applied for the matrix grain size.
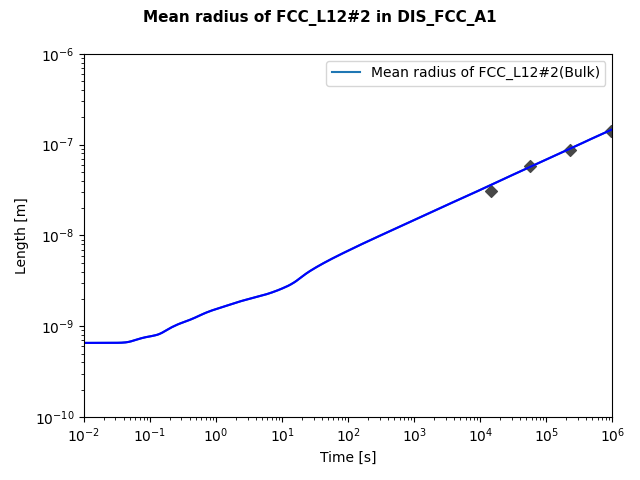
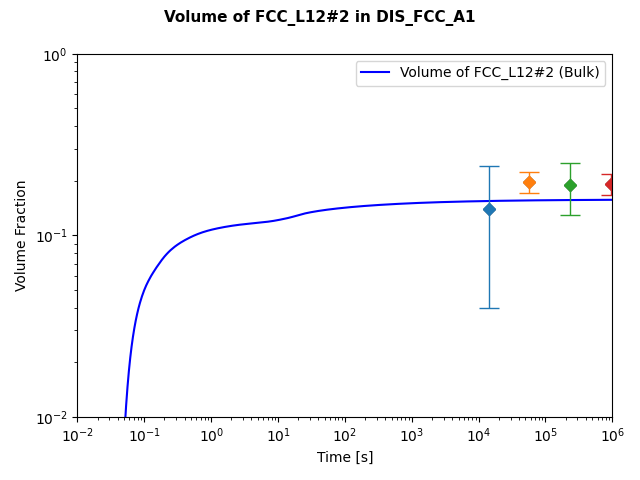
File name: pyex_P_07_Precipitation_Ni_Al_Cr_Isothermal_Gamma_Gamma.py
Also see the Graphical Mode example that this is based on: P_05: Precipitation of γ’ in Ni Superalloys - Isothermal
This example simulates the kinetics of precipitation of gamma prime (γ’) phase from gamma (γ) phase. The simulation results can be compared with experimental data collected from Sudbrack et al. [2008Sud].
This plot shows the results of an isothermal calculation to plot the mean radius of the cementite phase.
This plot shows the results of an isothermal calculation to plot the volume fraction of the cementite phase.
This plot shows the results of an isothermal calculation to plot the number density of the cementite phase.
Reference
[2008Sud] C. K. Sudbrack, T. D. Ziebell, R. D. Noebe, D. N. Seidman, Effects of a tungsten addition on the morphological evolution, spatial correlations and temporal evolution of a model Ni–Al–Cr superalloy. Acta Mater. 56, 448–463 (2008)
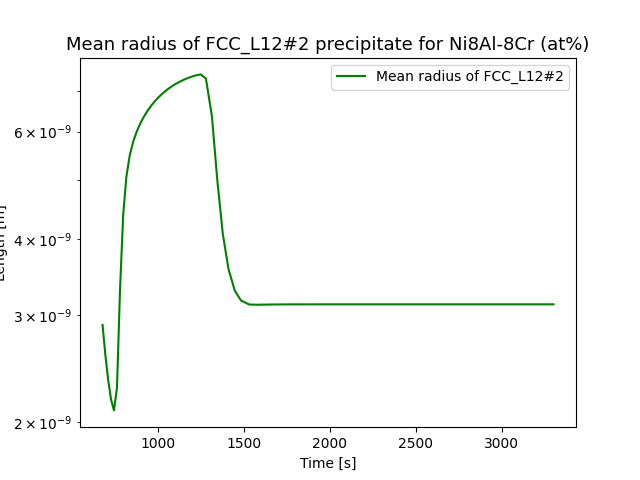
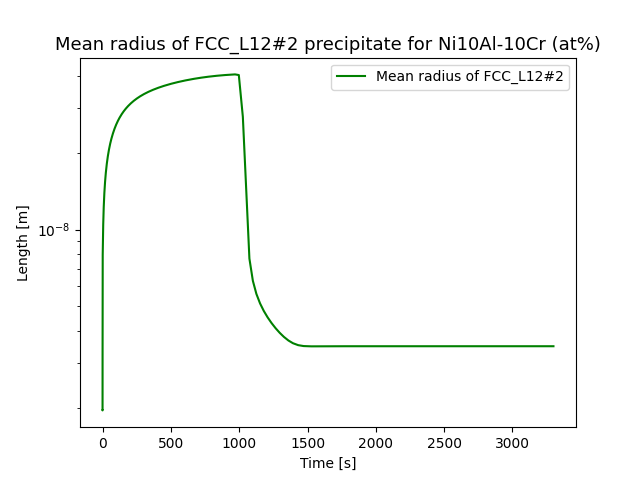
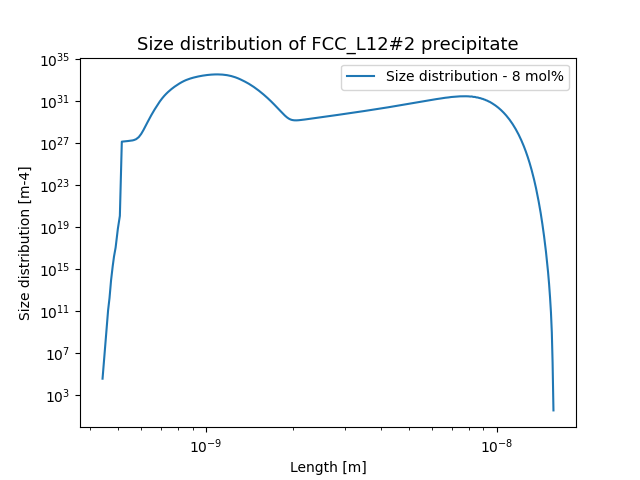
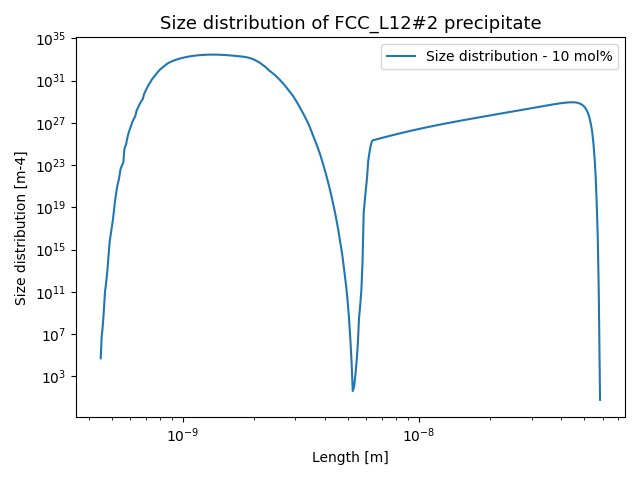
File name: pyex_P_08_Precipitation_Ni_Al_Cr_NonIsothermal.py
Also see the Graphical Mode example that this is based on: P_06: Precipitation of γ’ in Ni Superalloys - Non-isothermal
This example simulates the kinetics of precipitation of gamma prime (γ’) phase from gamma (γ) phase in Ni-8Al-8Cr and Ni-10Al-10Cr at.% alloys during continuous cooling. The simulation results can be compared with experimental results from Rojhirunsakool et al. [2013Roj].
Reference
[2013Roj] T. Rojhirunsakool, S. Meher, J. Y. Hwang, S. Nag, J. Tiley, R. Banerjee, Influence of composition on monomodal versus multimodal γ′ precipitation in Ni–Al–Cr alloys. J. Mater. Sci. 48, 825–831 (2013).
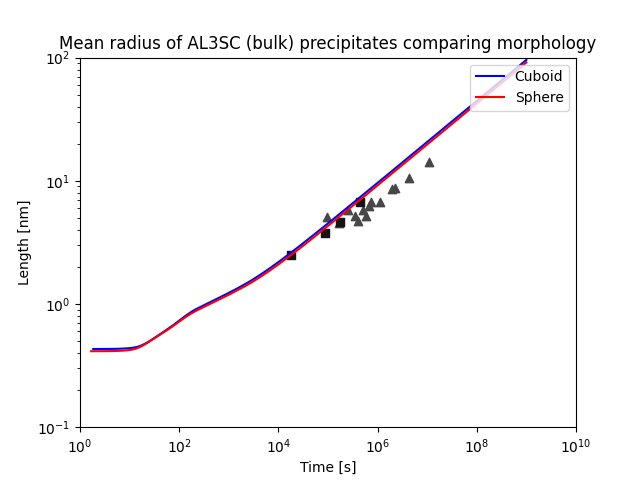
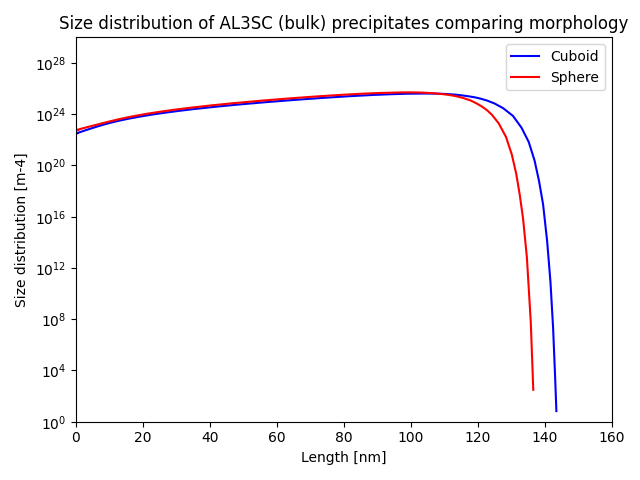
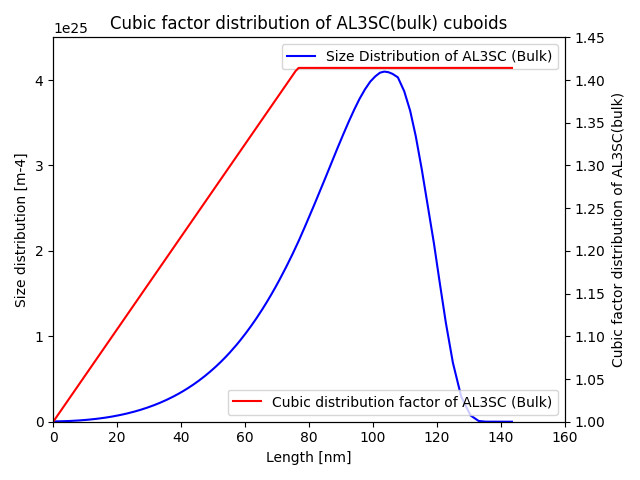
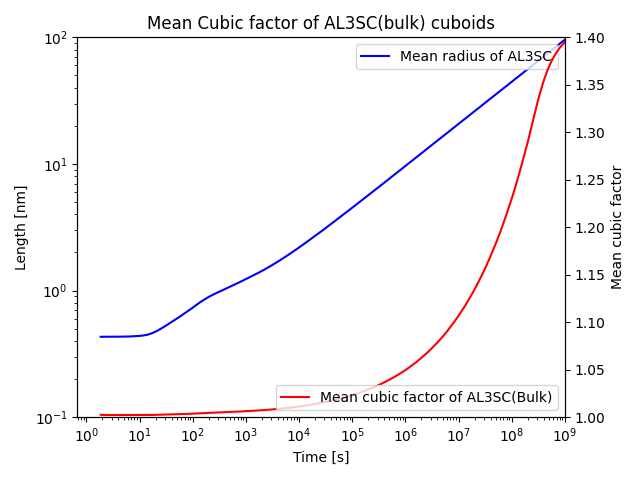
File name: pyex_P_09_Precipitation_Al_Sc_Sphere_Cuboid.py
Also see the Graphical Mode example that this is based on: P_09: Precipitation of Al-Sc AL3SC with Assumption of Sphere and Cuboid Morphologies
In this isothermal calculation example, the simulation of Al3Sc phase precipitation in an Al-Sc binary alloy is carried out. Two calculations are conducted: one assumes a spherical morphology without elastic strain energy, while the other assumes a cuboid shape determined by the interplay between interfacial energy and elastic strain energy. The simulation results are then compared with experimental data collected from studies by Marquis and Seidman [2001Mar] and Novotny and Ardell [2001Nov].
References
[2001Mar] E. A. Marquis, D. N. Seidman, Nanoscale structural evolution of Al3Sc precipitates in Al(Sc) alloys. Acta Mater. 49, 1909–1919 (2001).
[2001Nov] G. M. Novotny, A. J. Ardell, Precipitation of Al3Sc in binary Al–Sc alloys. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 318, 144–154 (2001).
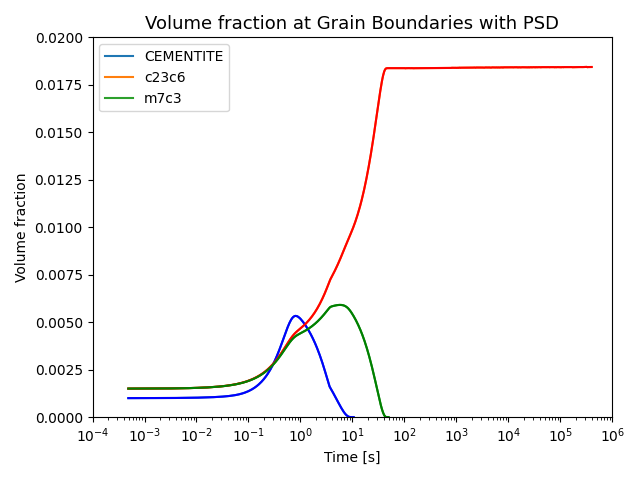
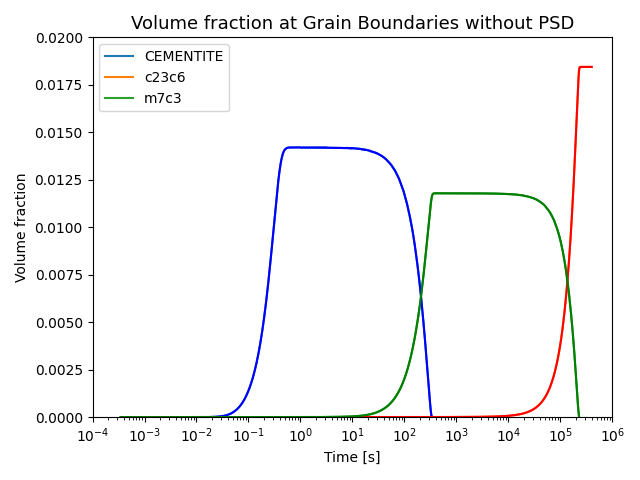
File name: pyex_P_10_Precipitation_Intitial_PSD_FeCrC.py
Also see the Graphical Mode example that this is based on: P_10: Initial Particle Size Distribution of Fe-Cr-C
In this example, the effect of the initial particle size distribution (PSD) on overall precipitation kinetics is demonstrated. Two Precipitation Calculators are utilized to simulate and compare carbide precipitations in a Fe-0.1C-12Cr alloy within a ferritic BCC_A2 matrix. Competitive precipitations involving three carbides, CEMENTITE, M23C6, and M7C3, are analyzed, and the precipitation kinetics are compared in terms of the presence or absence of the initial particle size distribution.
File name: pyex_P_11_Interfacial_Energy.py
Also see the Graphical Mode example that this is based on: P_11: Interfacial Energy Function
At four temperature points (673 K, 703 K, 733 K, and 763 K), this isothermal calculation employs four Precipitation Calculators, each 30 K apart. It aims to investigate the mean radius of an Al-0.12Sc system with an FCC_A1 matrix phase and AL3SC precipitate phase featuring bulk nucleation sites.
Notably, the user defines the interfacial energy function, utilizing an error function for a smooth transition of interfacial energy, transitioning from 0.065 J/m2 to 0.085 J/m2 based on particle radii, distinguishing between values below and above 1e-8m and 5e-8m, respectively.
A dataset based on Iwamura and Miura [2004Iwa] data is compared with the calculated results.
The results of an isothermal calculation to examine the mean radius of an Al-0.12Sc system with experimental data.
Reference
[2004Iwa] S. Iwamura and Y. Miura, “Loss in coherency and coarsening behavior of Al3Sc precipitates,” Acta Mater., vol. 52, no. 3, pp. 591–600, 2004.
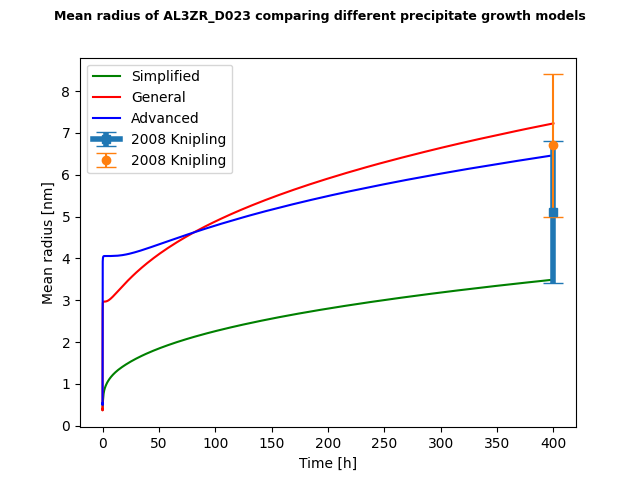
File name: pyex_P_12_Precipitation_Al_Zr_Growth_Rate_Model_Comparison.py
Also see the Graphical Mode example that this is based on: P_12: Comparing Growth Rate Models for an Al-Zr System
This example simulates the kinetics of precipitation of AL3ZR_D023 from an FCC_A1 solution phase. Three different precipitate growth models are compared, Simplified, General and Advanced. See online help for more information about the growth models. A dataset based on Knipling et al. [2008Kni] data is compared with the calculated results.
Result comparing the mean radius of the spheres for each AL3ZR_D023 precipitate phase calculated for each type of growth rate model.
Reference
[2008Kni] K. E. Knipling, D. C. Dunand, D. N. Seidman, Precipitation evolution in Al–Zr and Al–Zr–Ti alloys during isothermal aging at 375–425°C. Acta Mater. 56, 114–127 (2008).
File name: pyex_P_13_Precipitation_Fe_C_Cr_Paraequilibrium_Precipitation_of_Cementite.py
Also see the Graphical Mode example that this is based on: P_13: Paraequilibrium Precipitation of Cementite Fe-C-Cr
In this example, the precipitation of cementite during tempering of a Fe-Cr-C steel is simulated considering two interface conditions: one is the usual ortho-equilibrium condition; the other is the paraequilibrium condition. The simulation results are compared with the experimental data from Sakuma et al. [1980Sak].
Reference
[1980Sak] T. Sakuma, N. Watanabe, T. Nishizawa, The Effect of Alloying Element on the Coarsening Behavior of Cementite Particles in Ferrite. Trans. Japan Inst. Met. 21, 159–168 (1980).
File name: pyex_P_15_Fe_C_Mn_PE_OE_Precipitation_of_Cementite.py
Also see the Graphical Mode example that this is based on: P_15: Smooth Transition from Paraequilibrium to Ortho-equilibrium
In this example, the precipitation of cementite during tempering of an Fe-Mn-C steel is simulated considering three interface conditions: the usual ortho-equilibrium (OE) condition; paraequilibrium (PE) condition; and a smooth transition from paraequilibrium to ortho-equilibrium condition (PE-OE). The simulation results are compared with the experimental data from Miyamoto et al. [2007Miy].
Reference
[2007Miy] G. Miyamoto, J. Oh, K. Hono, T. Furuhara, T. Maki, Effect of partitioning of Mn and Si on the growth kinetics of cementite in tempered Fe–0.6 mass% C martensite. Acta Mater. 55, 5027–5038 (2007).
![pyex_P_07: Precipitation NiAlCr IsothermalFile name: pyex_P_07_Precipitation_Ni_Al_Cr_Isothermal_Gamma_Gamma.pyAlso see the Graphical Mode example that this is based on: P_05: Precipitation of γ’ in Ni Superalloys - IsothermalThis example simulates the kinetics of precipitation of gamma prime (γ’) phase from gamma (γ) phase. The simulation results can be compared with experimental data collected from Sudbrack et al. [2008Sud].This plot shows the results of an isothermal calculation to plot the mean radius of the cementite phase. This plot shows the results of an isothermal calculation to plot the volume fraction of the cementite phase.This plot shows the results of an isothermal calculation to plot the number density of the cementite phaseReference [2008Sud] C. K. Sudbrack, T. D. Ziebell, R. D. Noebe, D. N. Seidman, Effects of a tungsten addition on the morphological evolution, spatial correlations and temporal evolution of a model Ni–Al–Cr superalloy. Acta Mater. 56, 448–463 (2008) pyex_P_07: Precipitation NiAlCr IsothermalFile name: pyex_P_07_Precipitation_Ni_Al_Cr_Isothermal_Gamma_Gamma.pyAlso see the Graphical Mode example that this is based on: P_05: Precipitation of γ’ in Ni Superalloys - IsothermalThis example simulates the kinetics of precipitation of gamma prime (γ’) phase from gamma (γ) phase. The simulation results can be compared with experimental data collected from Sudbrack et al. [2008Sud].This plot shows the results of an isothermal calculation to plot the mean radius of the cementite phase. This plot shows the results of an isothermal calculation to plot the volume fraction of the cementite phase.This plot shows the results of an isothermal calculation to plot the number density of the cementite phaseReference [2008Sud] C. K. Sudbrack, T. D. Ziebell, R. D. Noebe, D. N. Seidman, Effects of a tungsten addition on the morphological evolution, spatial correlations and temporal evolution of a model Ni–Al–Cr superalloy. Acta Mater. 56, 448–463 (2008)](../resources/images/tc-python/examples/pyex_p_07_figure_3.png)