Coarsening

Physically speaking, coarsening or Ostwald ripening where big particles grow and small particles shrink is a process driven by lowering the total surface energy of the system. From a thermodynamic point of view, the Gibbs-Thomson effect leads to inhomogeneous chemical potentials in the system if the particle sizes are not uniform. Solutes at the interface in the matrix near a particle of a radius smaller than critical radius have a higher chemical potential than that corresponding to the mean concentration of the matrix. As a result, the solutes diffuse from the precipitate/matrix interface to the inside of the matrix and cause dissolution of the particle. Conversely, particles with a radius larger than the critical size have lower interface potentials, and the solutes diffuse to the interface and cause growth of the particles.

Since it is not possible to find a closed form analytic solution for the problem of diffusion-controlled spherical particle dissolution [1970Aar], we simply apply the Growth equations 1 to 5 with the absolute value of 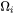to calculate the interface velocity for particles of all sizes.

As can be easily seen, if 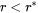, then the Gibbs-Thomson Equation 1 gives 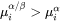, and a negative velocity results from Equation 2 for particles having , which means that they shrink.

Results for particles having 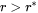are obtained vice versa. In all situations, when the absolute values of  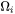are very small, the steady-state solution for either growth or dissolution are recovered. In conclusion, the dissolution is treated as the reverse of growth (1970Aar, Ibid.), and the coarsening comes out naturally either together with nucleation and growth or as a dominant process finally in the course of the evolution of the PSD.

Reference

[1970Aar] H. B. Aaron, Diffusion-Limited Phase Transformations: A Comparison and Critical Evaluation of the Mathematical Approximations. J. Appl. Phys. 41, 4404 (1970).