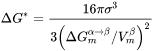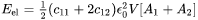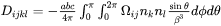Homogeneous Nucleation
The classic nucleation theory (CNT) [2000, Kashchiev; 1980, Russell] has been extended for the purpose of modeling nucleation in multicomponent alloy systems. The time-dependent nucleation rate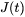 
is given by
[Eq. 1]
where
-
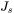is the steady state nucleation rate, -
is the incubation time for establishing steady state nucleation conditions, and -
is the time.
The steady state nucleation rate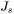 
is expressed by
[Eq. 2]
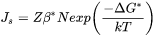
where
-
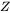is the Zeldovich factor, -
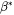is the rate at which atoms or molecules are attached to the critical nucleus, -
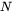is the number of available nucleation sites (of a particular type) per unit volume. In the case of homogeneous nucleation, initially, each atom in the whole volume of the mother phase is a potential nucleation site. As precipitation proceeds, the number of available nucleation sites decreases due to the occupancy of part of the matrix volume by formed secondary phase particles. In the case of heterogeneous nucleation, the initial number can also be estimated, given the grain size or dislocation density in the matrix phase. It decreases also with time but at different rates. -
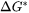is the Gibbs energy of formation of a critical nucleus, -
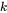is Boltzmann’s constant, -
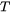is absolute temperature.
The Gibbs energy of formation of a critical nucleus is expressed as
where
-
is the interfacial energy, -
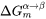is the molar Gibbs energy change for the formation of the β precipitate of the critical composition 
from the 
matrix, i.e. the maximum driving force for the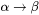 
phase transformation -
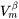is the molar volume of the β precipitate phase.
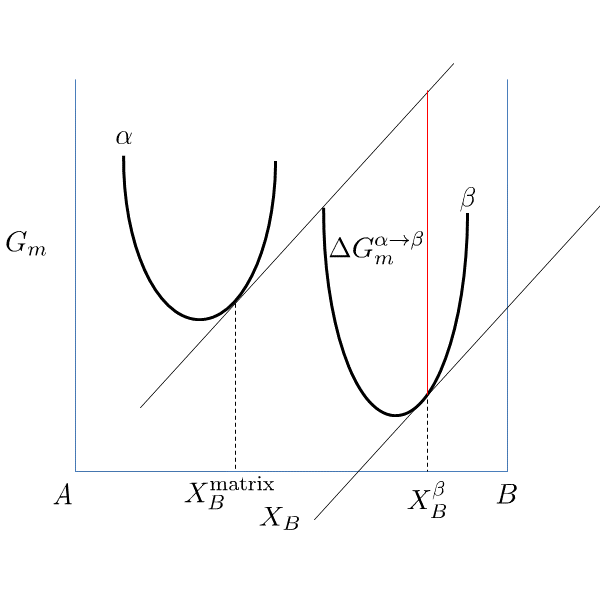
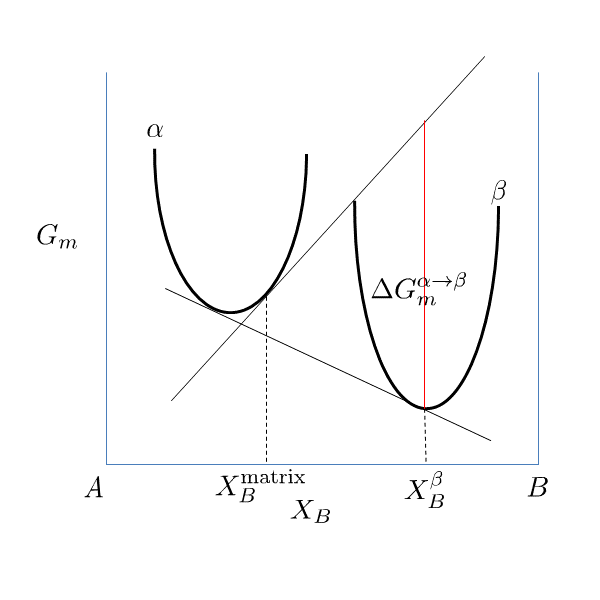
If elastic strain energy is excluded,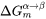 
is the chemical driving force for nucleation. There are two ways to calculate the nucleation driving force 
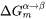and the critical composition 
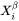, as shown in Figure 1 for a prototype binary system. The standard calculation in Figure 1 is to obtain the maximum driving force by finding the parallel tangent lines or surfaces passing through the alloy composition of the matrix, which is a routine calculation in the Thermo‑Calc software. The approximate calculation in Figure 1 is performed by using the Gibbs energy difference corresponding to the equilibrium composition in the precipitate phase. It can be used when the standard calculation fails, mostly within a miscibility gap. Additionally, the standard calculation is also used for driving force under paraequilibrium conditions, while the approximate calculation is used for driving force under NPLE (Non-Partitioning Local Equilibrium) conditions.
Figure 1: Methods to calculate the nucleation driving force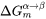 
and the critical composition 
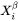. The standard calculation (left) and an approximate calculation (right).
Nucleation is a stochastic process and can be considered formally as a diffusion process or Brownian movement in the particle size space. Supercritical nuclei with radius slightly larger than the critical radius have a probability of passing back across the free energy barrier and dissolve in the matrix. The Zeldovich factor (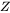
) is a measure of such probability and is related solely to the thermodynamics of the nucleation process in
[Eq. 4]
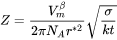
where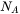 
is the Avogadro number and 
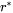, the critical radius, is given by
[Eq. 5]
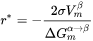
The atomic or molecular attachment rate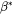 
reflects the kinetics of mass transport in the nucleation process and is given by Svoboda et al. [2004Svo].
[Eq. 6]
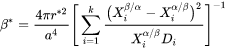
where
-
is the lattice parameter, -
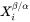and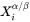 
are the mole fractions of element i at the interface in the precipitate and matrix, respectively. -
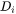is the corresponding diffusion coefficient in the matrix.
The incubation time 
for an isothermal reaction is
[Eq. 7]
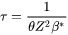
where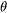 
differs from one derivation to another. The value 2 from Feder et al. [1966Fed] is adopted.
Elastic Strain Energy
Elastic strain energy,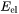 
, reduces the nucleation driving force, 
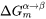in Eq. 3, hence affecting nucleation rate and nuclei size. It also changes the shape of the particle by competing with interfacial energy.
Cuboid Particle
The numerical simulations by Onaka et al. [2003Ona] indicate that the elastic strain energy is reduced almost linearly with increasing cubic factor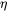 
. Since the numerical simulations are computationally expensive, we assume that the elastic strain energy follows the linear relationship with 
, and the elastic strain energy for spherical (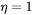
) and cubic (
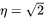) are calculated based on Khachaturyan’s approximation [1983/2008Kha].
where
-
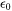is the lattice misfit strain, -
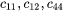are elastic constants in a cubic system, -
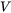is particle volume, -
and 
are expressed as
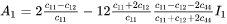
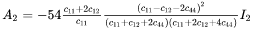
with
Sphere
Cubic
Ellipsoidal Particle (Plate and Needle)
Since they are ellipsoidal shape, it is convenient to use Eshelby’s theory [1957/1959Esh] with a reasonable computational cost. The Eshelby’s tensor can be calculated by simply performing a surface integral over a unit sphere
where
-
are ellipsoid axes, -
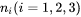are unit directional vector normal to the spherical surface and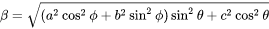 
For matrix phase with cubic crystal symmetry, we have for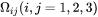 
. See [1983Kha].
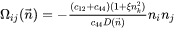
where
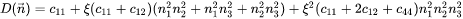
The Eshelby S tensor can then be calculated as
[Eq. 10]
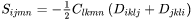
The total strain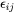 
at each location inside the particle is related to its transformation strain (eigenstrain) 
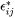as
[Eq. 11]
Combined with elastic stress calculated as
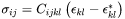
The elastic strain energy can be then obtained
[Eq. 12]
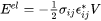
with 
the particle volume.
Spherical Approximation for Nuclei
In the Precipitation Module, the user-input or calculated interfacial energy is assumed to be the coherent interfacial energy that applies to the habit plane,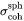 
, consistent with the approximation made by the embedded interfacial energy model. When calculating the critical nuclei, the interfacial energy in Eq. 3 is assumed to be that of a spherical particle with constant specific interfacial energy 
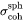. This is consistent with the fact that the nuclei tend to be spherical due to dominant interfacial energy. Interfacial energy penalty assuming a nucleus with pre-defined, and most likely large, aspect ratio is thus over-estimated, and has been found to shut down nucleation event abnormally.
Under spherical approximation, the elastic strain energy is calculated using spherical expression in Eq. 8 for spherical and cuboidal particles, or by setting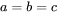 
in Eq. 9 for ellipsoidal particles.
References
[1957Esh] J. D. Eshelby, The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. A Math. Phys. Eng. Sci. 241, 376–396 (1957).
[1959Esh] J. D. Eshelby, The Elastic Field Outside an Ellipsoidal Inclusion. Proc. R. Soc. A Math. Phys. Eng. Sci. 252, 561–569 (1959).
[1966Fed] J. Feder, K. C. Russell, J. Lothe, G. M. Pound, Homogeneous nucleation and growth of droplets in vapours. Adv. Phys. 15, 111–178 (1966).
[1980Rus] K. C. Russell, Nucleation in solids: The induction and steady state effects. Adv. Colloid Interface Sci. 13, 205–318 (1980).
[2000Kas] D. Kashchiev. Nucleation. Butterworth-Heinemann, 2000.
[2003Ona] S. Onaka, N. Kobayashi, T. Fujii, M. Kato, Energy analysis with a superspherical shape approximation on the spherical to cubical shape transitions of coherent precipitates in cubic materials. Mater. Sci. Eng. A. 347, 42–49 (2003).
[2004Svo] J. Svoboda, F. D. Fischer, P. Fratzl, E. Kozeschnik, Modelling of kinetics in multi-component multi-phase systems with spherical precipitates. Mater. Sci. Eng. A. 385, 166–174 (2004).
[2013Kha] A. G. Khachaturyan, “Habit Plane and Orientation Relations in Precipitates: Comparison with Experimental Data.” in Theory of Structural Transformations in Solids (Dover Publications, Inc., New York, 2013.