Numerical Method
Since it is impossible to have a general close form solution, the complex non-linear continuity equation (see Continuity Equation) of the particle size distribution (PSD) function has to be solved numerically. Different numerical methods can be found in the literature to solve this equation, such as finite difference and method of characteristics. In all approaches, the continuous PSD is discretized into a sufficiently large number of size classes, and then integrated discretely in the time space. The Precipitation Module utilizes the method of characteristics, where the number of particles in each size class is kept constant unless particles of the same size have been nucleated.
An adaptive geometric grid allocation method has been used for particle size discretization since from nucleation to coarsening the particle size can span several orders of magnitude. In this approach, the new size grids are allocated evenly in a logarithmic scale and the number of grid points over one order of magnitude is kept almost constant during the whole process by class merging and splitting. The time step is controlled by several adjustable numerical parameters based on mechanistic quantities.
Summarized below are all numerical parameters used in this approach to control either the size grid distribution or time steps.
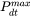
Maximum Time Step Fraction
Maximum time step allowed for time integration as fraction of the simulation time.
Number of Grid Points Over One Order of Magnitude in r
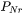
Default number of grid points for every order of magnitude in size space. The number determines a default ratio between two adjacent grid points. When there is a need to create new grid points, such as nucleating at a new radius not covered by the current range of PSD, this default ratio is used to add these new radius grid points. A larger value of this parameter enforces a finer grid to allow better numerical accuracy. However, this also comes with performance penalty, since finer grid in the size space often requires smaller time step to resolve the calculations.
Maximum Number of Grid Points Over One Order of Magnitude in r
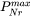
The maximum allowed number of grid points in size space. This parameter determines a lower bound limitation for the ratio of every two next nearest grid points in order to maintain adequate computational efficiency. When a ratio of two next nearest grid points is less than this limit, the middle grid point is removed and the corresponding size class merged with the two neighboring ones.
Minimum Number of Grid Points Over One Order of Magnitude in r
The minimum allowed number of grid points in size space. This parameter determines an upper bound limitation for the ratio of every two adjacent grid points in order to maintain proper numerical accuracy. When a ratio of two adjacent grid points exceeds this limit, a new grid point is then inserted between the two adjacent grids to keep the required resolution.
Maximum Relative Radius Change
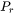
The maximum value allowed for relative radius change in one time step. This parameter limits the time step according to the following relation, which is controlled by the particle growth:
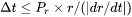for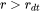 
where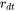 
is a cut-off subcritical size defined by the next parameter. The growth rates of supercritical particles (with 
) are always bounded, and there is a size class and the corresponding growth rate that controls the time step. The subcritical particles (with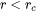 
), however, has a mathematical singularity (negative infinity) in growth rate as 
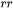approaches 0. This means that the time step can become extremely small if applying the above criterion to very small subcritical particles. In open literature, several researchers have tried mathematical transformation to avoid this singularity. Unfortunately, the transformation also complicates the formulation of the models. The Precipitation Module implementation uses a simple approach to deal with this issue by defining a cut-off size 
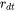. All the particles with 
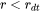may disappear within one time step. is determined by the next input parameter.
Maximum Relative Volume Fraction of Subcritical Particles Allowed to Dissolve in One Time Step
This parameter represents the portion of the volume fraction that can be ignored when determining the time step. It is used to calculate the cut-off subcritical size,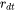 
, for the above time step control that allows a maximum relative radius changes for all particles:
Relative Radius Change for Avoiding Class Collision
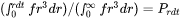
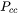
For the supercritical particles, the growth rate is non-linear – usually, it first increases with 
and then decreases after a certain size. In the region(s) with growth rate decreasing with 
, it is possible that the smaller size grid point can catch up with the larger size grid, if the time step is not controlled. To prevent this from happening, an additional parameter,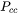 
, can be used to set a limit on time step according to the following relation:
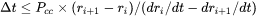
for
and
Maximum Overall Volume Change
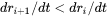
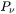
This parameter defines the maximum absolute (not ratio) change of the volume fraction allowed during one time step. This parameter is also used in controlling allowable variation in volume fraction due to the newly created particles within one time step. That is
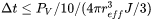
where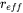 
and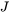 
are effective radius and nucleation rate, respectively.
Maximum Relative Change of Nucleation Rate in Logarithmic Scale
This parameter ensures accuracy for the evolution of effective nucleation rate. It sets a limit on time step so that the relative change of nucleation rate does not exceed the specified value, based on the information of previous step. That is
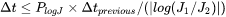
where nucleation rate 
and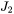 
occurs at the beginning and end of 
.
Maximum Relative Change of Critical Radius
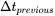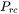
During the nucleation under high supersaturation, the critical radius can vary dramatically. Hence, this parameter can be used to place a constraint on how fast the critical radium can vary, and thus put a limit on time step:
Minimum Radius for a Nucleus to be Considered as a Particle
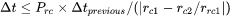
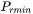
The cut-off lower limit of precipitate radius. Particles with radius smaller than the value specified for this parameter are discarded. In reality, the particle cannot be smaller than an atom; hence, there is no reason to keep track of particles of unphysical sizes.
Maximum Time Step During Heating Stages
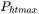
The upper limit of the time step that has been enforced in the heating stages. The current algorithm may over-estimate the subsequent time increment when temperature is increased. It is thus required to reduce this value when the calculation terminates unexpectedly during or after a heating stage.
Numerical Control Parameters Default Values
Default value for numerical parameters that controls the size grid distribution and time step.
| Parameter |
Default value |
|---|---|
|
0.1 |
|
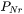
200 |
|
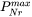
300 |
|
100 |
|
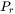
0.01 |
|
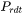
0.01 |
|
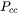
0.5 |
|
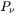
0.001 |
|
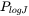
0.5 |
|
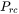
0.1 |
|
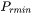
5e-10m |
|
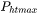
1.0s |