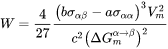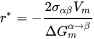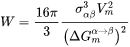Heterogeneous Nucleation
All equations remain the same for the calculation of heterogeneous nucleation rate within the framework of classic nucleation theory (CNT), but the nucleation energy and available nucleation site are different.
To a first approximation, the nucleation energy may be calculated by assuming an effective interfacial energy for each heterogeneous nucleation site.
For a rigorous treatment of heterogeneous nucleation the effect of wetting angles need to be considered.
Non-Spherical Particles and the Effect of Wetting Angle
Precipitation Module (TC-PRISMA) References
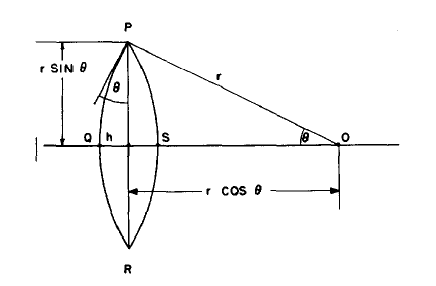
Non-spherical particles have been considered for grain boundary (GB) precipitation. Three morphologies are implemented for grain boundary, grain edge and grain corner precipitation, respectively, as shown in Figure 1. The parameter that defines the deviation from spherical shape is wetting angle (or dihedral angle), 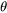 , as described in Figure 2 and taken from Clemm and Fisher [1955Cle].
, as described in Figure 2 and taken from Clemm and Fisher [1955Cle].
(a) (b) (c)
Figure 1: Non-spherical particles (β) that precipitate at grain boundaries of matrix phase( ) (a) grain boundary (two-grain junction) (b) grain edge (three-grain junction) (c) grain corners (four-grain junction). Images from [2004Zan].
) (a) grain boundary (two-grain junction) (b) grain edge (three-grain junction) (c) grain corners (four-grain junction). Images from [2004Zan].
Figure 2: The nucleus at the grain boundary. Image from [1955Clem].
Some physical parameters, mainly in nucleation models, have to be modified for the effect of the wetting angle. The following discussions contribute to this effect.
Shape Factors
Following Clemm and Fisher, the eliminated grain boundary area between  grains due to the formation of nucleus of a new phase β is:
grains due to the formation of nucleus of a new phase β is:
Where  is the radius of curvature of the nucleus. The surface area of the nucleus is:
is the radius of curvature of the nucleus. The surface area of the nucleus is:
[Eq. 2]
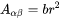
and the volume of the nucleus is
The expression of  ,
,  ,
,  in Eq. 1 and Eq. 3 for grain boundary (two-grain junction), grain edge (three-grain junction) and grain corner (four-grain junction) can be found in the paper by Clemm and Fisher [1955Cle].
in Eq. 1 and Eq. 3 for grain boundary (two-grain junction), grain edge (three-grain junction) and grain corner (four-grain junction) can be found in the paper by Clemm and Fisher [1955Cle].
Critical Radius and Activation Energy
The energy change due to the formation of the new particle is thus
[Eq. 4]

where 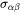 and
and 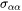 are the interfacial energy and grain boundary energy, respectively.
are the interfacial energy and grain boundary energy, respectively.
Then the critical radius should be
And the activation energy barrier for nucleation is
The interfacial energy, grain boundary energy and wetting angle can be related as
[Eq. 7]

i.e.
[Eq. 8]
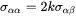
which can be replaced into Eq. 5 and Eq. 6.
[Eq. 9]
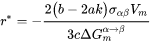
[Eq. 10]
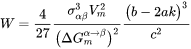
The bulk, spherical precipitation equation is recovered by:
[Eq. 11]
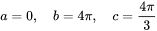
so that
And also the grain boundary precipitation with spherical shape (with weighting angle 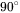 ) follows Eq. 12 and Eq. 13 by
) follows Eq. 12 and Eq. 13 by 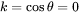 .
.
Zeldovich Factor
The Zeldovich factor is modified as
[Eq. 14]
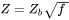
with 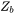 the original value, and
the original value, and 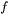 the volume factor that is the ratio of the
the volume factor that is the ratio of the  in Eq. 3 to the spherical shape factor
in Eq. 3 to the spherical shape factor 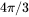 .
.
[Eq. 15]

Impingement Rate
The surface area factor in impingement rate calculation is changed from 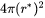 to
to  .
.
Nucleation Site Density
In each time step, the occupied grain boundary area
[Eq. 16]

is deducted when calculating available nucleation site density.
Growth Rate
The radius  defined in previous equations is the curvature of the precipitate surface (the Big radius) as shown in Figure 2. It is exactly the definition in the growth rate whose coarsening consideration relates to the curvature effect. Therefore, the growth rate equation can be directly used with
defined in previous equations is the curvature of the precipitate surface (the Big radius) as shown in Figure 2. It is exactly the definition in the growth rate whose coarsening consideration relates to the curvature effect. Therefore, the growth rate equation can be directly used with  being defined here. Again, for bulk, spherical precipitation it automatically corresponds to the particle radius.
being defined here. Again, for bulk, spherical precipitation it automatically corresponds to the particle radius.
Output
The volume of the precipitate should be calculated appropriately as 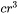 with
with  being the curvature of the particle surface as defined above. For output of the particle size (mean radius, critical radius and particle size distribution) in the user interface, it seems better to use the radius of the eliminated grain boundary area, i.e.
being the curvature of the particle surface as defined above. For output of the particle size (mean radius, critical radius and particle size distribution) in the user interface, it seems better to use the radius of the eliminated grain boundary area, i.e.
[Eq. 17]
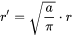
With  defined in Eq. 1.
defined in Eq. 1.
For example, the size of the precipitate at grain boundary (two-grain junction) is the radius of the lens shown in Figure 2.
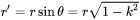
The Number of Available Heterogeneous Nucleation Sites
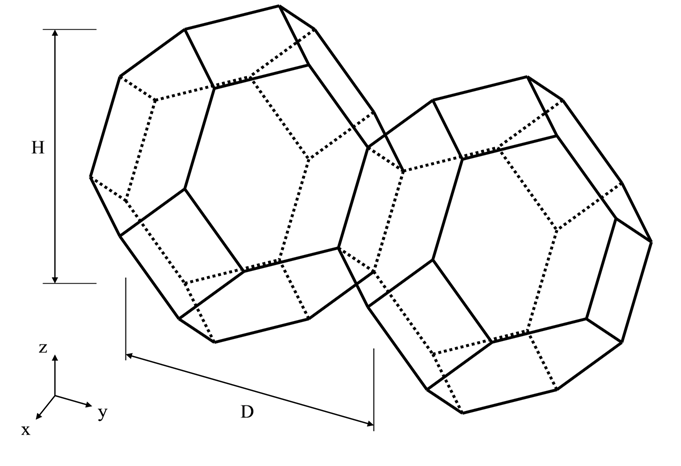
Figure 3: An example of tetrakaidecahedron approximation of grains.
The number of different nucleation sites is dependent on the shape and size of grains in the matrix. Assuming all grains are equally large tetrakaidecahedra with the distance between one pair of square faces as H, and that between the other two pairs as D we obtain the densities 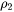 ,
, 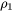 , and
, and 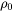 for the grain boundary area, edge length, and grain corner number, respectively in
for the grain boundary area, edge length, and grain corner number, respectively in
[Eq. 18]

[Eq. 19]
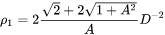
[Eq. 20]
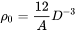
where  is the aspect ratio, defining the degree of elongation of the grains.
is the aspect ratio, defining the degree of elongation of the grains.
By default, the aspect ratio is set to 1 and the densities are then the same as obtained by Cahn [1956Cah]. Once the densities are known, if taking boundary thickness as one atomic layer, the available nucleation sites can be calculated by
[Eq. 21]

where  is the molar volume of the matrix phase and
is the molar volume of the matrix phase and 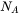 is the Avogadro number.
is the Avogadro number.
For a crystalline material, given a dislocation density 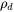 , the number of nucleation sites at the dislocations
, the number of nucleation sites at the dislocations 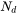 can be calculated with the same form as in
can be calculated with the same form as in
[Eq. 22]

References
[1955Cle] P. J. Clemm, J. C. Fisher, The influence of grain boundaries on the nucleation of secondary phases. Acta Metall. 3, 70–73 (1955).
[1956Cah] J. W. Cahn, Transformation kinetics during continuous cooling. Acta Metall. 4, 572–575 (1956).
[2004Zan] L. Zang, Lecture 13: Heterogeneous Nucleation: Effects of Grain Boundaries and Surface Defects, The University of Utah, (2004), (available at http://www.eng.utah.edu/%7B$~$%7Dlzang/images/lecture-13.pdf).