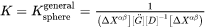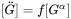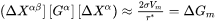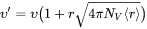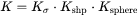Growth
Spherical Particles
The growth rate models implemented in the Precipitation Module are called Advanced, Simplified, General, Para-eq, NPLE, and PE Automatic. All models treat a spherical particle (precipitate) of stoichiometric composition or with negligible atomic diffusivity.
All models treat a particle (precipitate) of stoichiometric composition or with negligible atomic diffusivity. Except for the PE Automatic model, local equilibrium or paraequilibrium at the precipitate-matrix interface is assumed. The PE Automatic model enables smooth transition from paraequilibrium to local equilibrium.
In the documentation and on the GUI, the abbreviations Para-eq and PE are both used for paraequilibrium. There is also the use of OE as an abbreviation for ortho-equilibrium and LE for local equilibrium.
Advanced Growth Rate Model
The Advanced model is proposed by Chen, Jeppsson, and Ågren (CJA) [2008Che]. In this model, the velocity of a moving phase interface and the operating tie-line are solved together from flux-balance equations. This model can treat both high supersaturation and cross diffusion rigorously. It can also capture the transition between NPLE (non-partitioning local equilibrium) and PLE (partitioning local equilibrium) without any ad hoc treatment.
According to the CJA model, the interface velocity  can be obtained together with interface concentrations by numerically solving
can be obtained together with interface concentrations by numerically solving 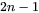 equations, comprising of the flux balance equations for
equations, comprising of the flux balance equations for 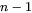 independent components and the local equilibrium conditions for all
independent components and the local equilibrium conditions for all  components as in
components as in
where
-
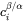 and
and 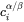 are the volume concentrations of component
are the volume concentrations of component  at the interface in the precipitate and matrix, respectively,
at the interface in the precipitate and matrix, respectively, -
 is the corresponding atomic mobility in the matrix,
is the corresponding atomic mobility in the matrix, -
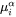 and
and 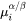 are the chemical potentials in the matrix of the mean-field concentration and at the interface, respectively.
are the chemical potentials in the matrix of the mean-field concentration and at the interface, respectively. -
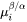 is the chemical potential at the interface in the precipitate.
is the chemical potential at the interface in the precipitate.
In the above local equilibrium condition, the multicomponent Gibbs-Thomson effect has been taken into account by adding a curvature induced pressure term to the Gibbs energy of the precipitate phase.
The introduced effective diffusion distance factor, 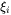 , for each independent component is given by
, for each independent component is given by
where
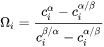
is the so-called dimensionless supersaturation for an individual component, and  is obtained via
is obtained via
[Eq. 4]
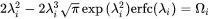
Simplified Growth Rate Model
In some cases, the Advanced model fails to find the solution to flux-balance equations. Even when it does, the calculation can be time consuming. Therefore, a simple and efficient, albeit less rigorous, model is preferred in many applications. The Simplified model [2022Ågr], in a pseudo-steady state approximation, is developed by solving Laplace equation along radial direction, and is expressed as
where 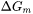 is the nucleation driving force and
is the nucleation driving force and 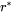 is the radius of critical nuclei.
is the radius of critical nuclei. 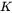 is the kinetic parameter that is related to solute composition and mobility. Neglecting cross diffusion, it is expressed as
is the kinetic parameter that is related to solute composition and mobility. Neglecting cross diffusion, it is expressed as
The interface compositions (mole fractions) 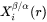 and
and 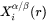 for precipitate and matrix phase, respectively, are tie-line compositions across the matrix composition. To avoid time-consuming equilibrium calculations and also realizing that precipitate composition
for precipitate and matrix phase, respectively, are tie-line compositions across the matrix composition. To avoid time-consuming equilibrium calculations and also realizing that precipitate composition 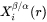 only appears in the difference term
only appears in the difference term
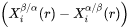
Equation 6 is further simplified by replacing 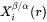 with nuclei composition from nucleation driving force calculation, and
with nuclei composition from nucleation driving force calculation, and  with matrix composition.
with matrix composition.
The 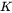 constant defined here relates growth rate to driving force in
constant defined here relates growth rate to driving force in 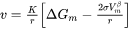 , which is not to be confused with coarsening rate constant relating mean particle radius cubed to time.
, which is not to be confused with coarsening rate constant relating mean particle radius cubed to time.
For the Precipitation Calculator → Precipitate Phase settings, Phase energy addition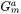 and Phase boundary mobility
and Phase boundary mobility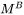 shifts the Gibbs energy of the precipitate
shifts the Gibbs energy of the precipitate 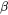 phase by
phase by 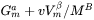 . As a result, the driving force
. As a result, the driving force 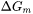 is reduced by
is reduced by 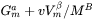 , and the equilibrium compositions
, and the equilibrium compositions 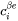 and
and 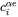 are shifted.
are shifted.
General Growth Rate Model
The General model is based on the existing coarsening models [1993Uma; 1994Mor; 1995Mor], which follows the same quasi-steady state approximation as the Simplified model, but improves by taking into account the cross diffusion. The growth rate equation has thus the same format as that in the Simplified model, i.e., Eq. 5, with the kinetic parameter 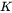 defined as
defined as
where 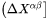 and
and 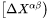 are
are  row and column vector, respectively, whose ith element is the composition difference
row and column vector, respectively, whose ith element is the composition difference 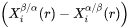 as described in Eq. 6.
as described in Eq. 6.  , a
, a 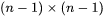 matrix, is based on thermodynamic factor matrix
matrix, is based on thermodynamic factor matrix 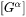 with a correction factor
with a correction factor
where thermodynamic factor matrix is defined as the secondary derivative of free energy with respect to composition in the matrix phase
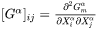
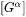 is evaluated at the far-field matrix composition to consider the multicomponent Gibbs-Thomson effect [1995Mor]. For a particle with critical nuclei size
is evaluated at the far-field matrix composition to consider the multicomponent Gibbs-Thomson effect [1995Mor]. For a particle with critical nuclei size  , the Gibbs-Thomson equation is
, the Gibbs-Thomson equation is
where 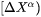 is a
is a 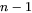 column vector representing the difference between the far-field matrix composition
column vector representing the difference between the far-field matrix composition 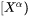 and the equilibrium (tie-line) composition of the matrix phase
and the equilibrium (tie-line) composition of the matrix phase 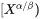 . It has been found that Eq. 9 is not numerically accurate and sometimes the deviation can be quite significant. Therefore, a correction factor is introduced as
. It has been found that Eq. 9 is not numerically accurate and sometimes the deviation can be quite significant. Therefore, a correction factor is introduced as
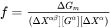
which then appears in Eq. 8.
 in Eq. 7 is the inverse of the chemical diffusivity matrix
in Eq. 7 is the inverse of the chemical diffusivity matrix  . In some alloy systems, diffusivity is strongly composition dependent, so that an effective diffusivity is necessary. A series of numerical simulations in comparison with DICTRA calculations indicates that a good approximation can be achieved if
. In some alloy systems, diffusivity is strongly composition dependent, so that an effective diffusivity is necessary. A series of numerical simulations in comparison with DICTRA calculations indicates that a good approximation can be achieved if 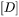 is the arithmetic mean of the diffusivity with far-field matrix composition and diffusivity with equilibrium (tie-line) composition
is the arithmetic mean of the diffusivity with far-field matrix composition and diffusivity with equilibrium (tie-line) composition
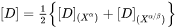
Paraequilibrium Growth Rate Model
The paraequilbrium (Para-eq) growth rate model is only available for alloy systems where Fe is the major element and C is the only interstitial element, which also partitions into the precipitate phase.
The intersitial elements, e.g. C, N, etc., usually have remarkably faster diffusion rate than the substitutional elements. Meanwhile, they are assumed to have negligible volume contribution, and as a result the composition variables in Eq. 6 to Eq. 9 are replaced by u-fractions when interstitial elements are included in the system. The paraequilbrium growth rate model is designed specifically to address the fast diffusion of C in Fe alloys. Based on the Simplified growth rate model, it holds a paraequilbrium condition [1953Hil] at the migrating interface, in that, instead of assuming that all alloying elements are in equilibrium at the interface as the regular ortho-equilibrium condition states, only C assumes equilibrium state, while the substitutional elements are immobile and thus have the same compositions (u-fractions) across the interface. Therefore, only composition of C and its mobility appear in Eq. 6.
PE Automatic Growth Rate Model
The tempering of martensite in steels induces the precipitation of cementite particles. The growth kinetics initially follows the paraequilbrium (abbreviated here as PE) condition due to the fast diffusion of interstitial C, and gradually transforms to regular Local Equilibrium (LE), i.e. Ortho-equilibrium (OE), condition so that substitutional elements can reach equilibrium partitioning at the migrating interface. The PE Automatic model enables the smooth transition from Paraequilibrium growth rate model to Simplified growth rate model. The rate of transition process is dependent on the relative differences in diffusion between C and substitutional elements, as well as the differences in driving force between PE and OE.
NPLE Growth Rate Model
The Non-Partitioning Local Equilibrium (NPLE) growth rate model is only available for alloy systems where Fe is the major element and at least one interstitial element partitions into the precipitate phase.
The NPLE growth model is designed specially to deal with the fast diffusion of interstitial element (C, N, etc.) in Fe alloys. Based on the Simplified growth model, it still holds a local equilibrium condition at the migrating interface, but chooses a tie-line under NPLE condition [1958Kir] that the u-fractions of all substitutional elements and minor interstitial elements in the precipitate phase are the same as those in the far-field matrix phase (i.e. the overall instantaneous matrix composition).
Model Selections
The most efficient model is the Simplified model, which is the default and applicable to most alloy systems under conditions that either the supersaturation is small, or the alloying elements have comparable diffusivity. If all alloying elements are substitutional but they have remarkable diffusivity difference, e.g. in Al-Zr system, or the diffusivity is strongly composition dependent, the General model is preferred. If the supersaturation is high, and meanwhile there are fast-diffusing interstitial elements such as C, the Advanced model is more appropriate to capture the NPLE mechanism.
In some cases with the General model, you may need to switch to another model if the matrix composition passes through a spinodal composition space where the thermodynamic factor becomes negative, thus leading to an abnormal growth rate. When this happens, Thermo‑Calc alerts you that the Matrix Composition in Spinodal Zone. It is then recommended to switch to other models.
Non-Zero Volume Correction
The non-zero volume correction to the velocity according to Chen and Voorhees [1993Che] is taken into account and it follows as
where
-
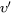 is the corrected velocity
is the corrected velocity -
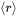 is the mean radius
is the mean radius -
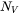 is the number density
is the number density
Non-Spherical Particles
A reference for this section can be found in [2018Wu].
Particle Shape Determination
The shape of the cuboid particles, the cubic factor, is determined by the minimization of combined interfacial energy and elastic strain energy. If you choose Calculated from molar volume for the Transformation strain as the Precipitation Calculator → Precipitate Phase settings, the lattice misfit is then calculated from difference in molar volume between matrix and precipitate phase, and the elastic strain energy is calculated accordingly. If you disregard the transformation strain, the elastic strain energy is neglected and hence the particles remain spherical in shape.
If you select the Calculated aspect ratio from elastic energy checkbox for either a plate or needle Morphology on the Precipitation Calculator → Precipitate Phase settings, the particle shape is determined by the minimization of combined interfacial energy and elastic strain energy. Otherwise, if you enter a value for aspect ratio, the particle shape is fixed except for nucleation calculation in which a spherical particle is always assumed.
Interfacial Energy Anisotropy
Isotropic interfacial energy is always assumed for spherical and cuboidal particles. For plate and needle, when the aspect ratio becomes larger than 1, the interfacial energy anisotropy occurs, so that the interfacial energy at the edge is larger than that at the broad face (habit plane). This increases the overall interfacial energy which is given as follows for each morphology.
Plate
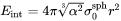
Needle
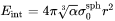
Where
-
 is the aspect ratio
is the aspect ratio -
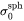 is the interfacial energy of the habit plane, i.e., the plane normal to the shorter axis
is the interfacial energy of the habit plane, i.e., the plane normal to the shorter axis -
 is the radius of a sphere with equivalent volume
is the radius of a sphere with equivalent volume
Growth Rate Adjustment
For non-spherical particles, the growth rate equations for spherical particles are still applicable, but adjustment parameters are introduced to take into account the shape effect. The cuboid particles arise from "symmetry preserving" transformation, e.g., FCC_A1 to L12 , and are thus highly isotropic and assumed growth rate equal to that of spherical particles. The plate and needle particles, on the other hand, arise from "symmetry breaking" transformations, e.g., cubic to tetragonal transformation, and are thus anisotropic leading to a significant increase of growth rate.
We define  as the radius of a sphere with equivalent volume of the non-spherical particle, so that the format of Eq. 5 keeps unchanged. In our current model, two effects are considered contributing to the growth rate for plate and needle particles, from interfacial energy anisotropy and particle shape effect. The kinetic parameter
as the radius of a sphere with equivalent volume of the non-spherical particle, so that the format of Eq. 5 keeps unchanged. In our current model, two effects are considered contributing to the growth rate for plate and needle particles, from interfacial energy anisotropy and particle shape effect. The kinetic parameter 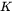 defined in Eq. 5 is thus given as
defined in Eq. 5 is thus given as
with  defined in Eq. 6 and Eq. 7. The interfacial energy
defined in Eq. 6 and Eq. 7. The interfacial energy  in Eq. 5 is that of habit plane, i.e., the plane that is normal to the shorter axis of the particle.
in Eq. 5 is that of habit plane, i.e., the plane that is normal to the shorter axis of the particle. 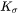 is the parameter that takes into account the Gibbs-Thomson effect due to interfacial energy anisotropy, based on Johnson [1965Joh].
is the parameter that takes into account the Gibbs-Thomson effect due to interfacial energy anisotropy, based on Johnson [1965Joh].
Plate
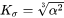
Needle
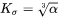
where  is the aspect ratio of the ellipsoidal particle.
is the aspect ratio of the ellipsoidal particle. 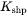 is the parameter that takes into account the non-spherical concentration field around the particle. Assuming a shape-conserving concentration field and thus following the derivation by Ham [1958 and 1959], it is given as
is the parameter that takes into account the non-spherical concentration field around the particle. Assuming a shape-conserving concentration field and thus following the derivation by Ham [1958 and 1959], it is given as
Plate
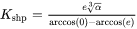
Needle
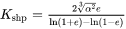
where  is the eccentricity of the ellipsoidal particle.
is the eccentricity of the ellipsoidal particle.
References
[1953Hil] M. Hillert, 1953. "Paraequilibrium." Internal Report, Swedish Institute for Metals Research.
[1958Ham] F. S. Ham, Theory of diffusion-limited precipitation. J. Phys. Chem. Solids. 6, 335–351 (1958).
[1958Kir] J. S. Kirkaldy, Diffusion in Multicomponent Metallic Systems: I. Phenomenological Theory for Substitutional Solid Solution Alloys. Can. J. Phys. 36, 899–906 (1958).
[1959Ham] F. S. Ham, Shape-preserving solutions of the time-dependent diffusion equation. Q. Appl. Math. 17, 137–145 (1959).
[1965Joh] C. A. Johnson, Generalization of the Gibbs-Thomson equation. Surf. Sci. 3, 429–444 (1965).
[1993, Chen] M. K. Chen, P. W. Voorhees, The dynamics of transient Ostwald ripening. Model. Simul. Mater. Sci. Eng. 1, 591–612 (1993).
[1993Uma] A. Umantsev, G. B. Olson, Ostwald ripening in multicomponent alloys. Scr. Metall. Mater. 29, 1135–1140 (1993).
[1994Mor] J. E. Morral, G. R. Purdy, Particle coarsening in binary and multicomponent alloys. Scr. Metall. Mater. 30, 905–908 (1994).
[1995Mor] J. E. Morral, G. R. Purdy, Thermodynamics of particle coarsening. J. Alloys Compd. 220, 132–135 (1995).
[2008Che] Q. Chen, J. Jeppsson, J. Ågren, Analytical treatment of diffusion during precipitate growth in multicomponent systems. Acta Mater. 56, 1890–1896 (2008).
[2018Wu] K. Wu, Q. Chen, P. Mason, Simulation of Precipitation Kinetics with Non-Spherical Particles. J. Phase Equilibria Diffus. 39, 571–583 (2018).
[2022Ågr] J. Ågren, Q. Chen, Simplified Growth Model for Multicomponent Systems - Inclusion of PARA and NPLE Conditions. J. Phase Equilibria Diffus., in press (2022).
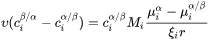

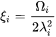
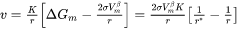


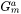 and “Phase boundary mobility”
and “Phase boundary mobility” 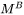 .
.