Zener Pinning

Zener [1948Smi] proposed a pinning force due to second-phase particles, so that the normal grain growth would be completely inhibited when the grain size reached a critical maximum grain size . In general form, it can be expressed as [1998Man]

[Eq. 1]         

Where

• is the radius of the pinning particles

• the volume fraction of the particles

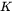• is a dimensionless constant

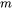• an exponential index for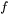

The original Zener pinning theory gives

which has been found to be inconsistent with the experimental information and thus needs refinement.

For simplicity, the average particle radius of a precipitate phase 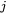has been used to calculate the pinning force arising from all the particles of this phase. The pinning force, 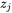, can be evaluated as the inverse of

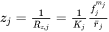
When there are multiple precipitate phases, the overall pinning effect is the sum of that from all precipitate particles,

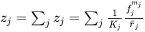
The retarding force due to Zener pinning, 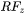, is therefore [1965Hil]

where is the grain boundary energy.

Realizing that the drag force resists the grain boundary motion, no matter in the growing (positive velocity) or shrinking (negative velocity) direction, the overall growth rate is expressed as [1965Hil]

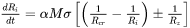
The negative sign holds when

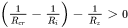
while positive sign holds when

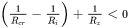
And 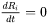when 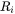lies between these two limits.

In the Precipitation Module (TC-PRISMA), you can input parameters 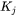and for each precipitate phase. An additional parameter, cutoff radius (unit= m), can be used so that precipitates with a smaller size than this value are excluded from the calculation of pinning force. This adjustment avoids an unreasonably large pinning force calculated from very small precipitates (e.g. nuclei).

P_14: Grain Growth and the Zener Pinning Effect

References

[1948Smi] C. S. Smith, Grains, Phases, and Interfaces - an Interpretation of Microstructure. Trans. AIME. 175, 15–51 (1948).

[1965Hil] M. Hillert, On the theory of normal and abnormal grain growth. Acta Metall. 13, 227–238 (1965).

[1998Man] P. A. Manohar, M. Ferry, T. Chandra, Five Decades of the Zener Equation. ISIJ Int. 38, 913–924 (1998).