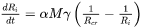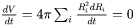Normal Grain Growth

The normal grain growth model in the Precipitation Module (TC-PRISMA) uses a similar approach to its precipitation counterpart (see Theory Overview) in that it calculates the temporal evolution of grain size distribution (GSD). The grains are assumed of spherical morphology when modeling the growth rates. Nucleation is not considered, thus an initial GSD is necessary to start the simulation.

The boundary motion of a grain with radius radius without considering pinning forces from precipitate particles, is driven by curvature and can be modeled as [1957Fel; 1965Hil]

[Eq. 1] equation for boundary motion of a grain with radius

where

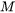is grain boundary mobility ()
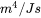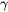is the grain boundary energy ()
is a dimensionless constant

If it should be satisfied that 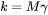, which is the parabolic growth rate of average grain size at steady-state

[Eq. 2] parabolic growth rate equation

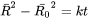
It was found that 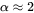alpha approx equals 2 [1965Hil].

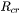in Eq. 1 is the critical grain size, which, not necessarily the average grain size, is determined by volume conservation [2008Jep]

[Eq. 3] Volume conservation equation

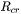where the index index covers all the grains at each time step. Substituting Eq. 1 into Eq. 3, critical grain size is obtained at each time step.

Grain Boundary Mobility Values

The grain boundary mobility 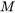can be calculated as:

[Eq. 4] equation for grain boundary mobility

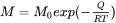
where

is the prefactor (m⁴/Js)
is the activation energy (J/mol)

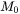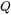The recommended values of Prefactor for grain boundary mobility and Activation energy for grain boundary mobility in high purity metals such as ferritic iron, austenitic iron, nickel, and aluminum are shown in the table below.

Since grain growth is significantly affected by grain boundary segregation, precipitation, and grain boundary complexion, the accuracy of the mobility data used for the recommended values is not guaranteed.

If the grain size is in nanoscale, these parameters may not be applicable since the effects of grain boundary junction and complexion cannot be ignored in nanocrystals. For some alloys, such as Al, the parameters can also be sensitive to temperature. The temperature range in the table is the suggested best fit.

Recommended grain growth parameters for mobility prefactor Prefactor for grain boundary mobility and activation energy Activation energy 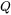for grain boundary mobility .

	Matrix Phase	Temperature Range (K)	Prefactor M₀ (m⁴/Js)	Activation Energy Q (J/mol)	Reference
High purity iron	BCC_A2	625 ~ 875	4E-3	242000	[1997Mal]
Low alloying steel (Cr-Mo)	FCC_A1	1173 ~ 1473	3.6E-3	228302	[2008Lee]
Pure Ni	DIS_FCC_A1/FCC_L12	1098 ~ 1323	4.12E-8	123050	[2008Ran]
High purity aluminum	FCC_A1	300 ~ 548	1.02E-14	27430	[2004Yu]
High purity aluminum	FCC_A1	573 ~ 773	1.25E-8	73080	[2004Yu]

References

[1957Fel] P. Feltham, Grain growth in metals. Acta Metall. 5, 97–105 (1957).

[1965Hil] M. Hillert, On the theory of normal and abnormal grain growth. Acta Metall. 13, 227–238 (1965).

[1997Mal] T. R. Malow, C. C. Koch, Grain growth in nanocrystalline iron prepared by mechanical attrition. Acta Mater. 45, 2177–2186 (1997).

[2004Yu] C. Y. Yu, P. L. Sun, P. W. Kao, C. P. Chang, Evolution of microstructure during annealing of a severely deformed aluminum. Mater. Sci. Eng. A. 366, 310–317 (2004).

[2008Jep] J. Jeppsson, J. Ågren, M. Hillert, Modified mean field models of normal grain growth. Acta Mater. 56, 5188–5201 (2008).

[2008Lee] S.-J. Lee, Y.-K. Lee, Prediction of austenite grain growth during austenitization of low alloy steels. Mater. Des. 29, 1840–1844 (2008).

[2008Ran] V. Randle, P. R. Rios, Y. Hu, Grain growth and twinning in nickel. Scr. Mater. 58, 130–133 (2008).