T_06: Serially Coupled Equilibrium Calculators

Sometimes there are multiple solutions for a given set of equilibrium conditions. In other cases the equilibrium calculation does not converge. You can then aid the final calculation by, in effect, telling the software where it should start the search for the equilibrium.

This example shows how to serially couple two Equilibrium Calculator nodes together for more complex equilibrium conditions. For each calculation, the output is to a Table Renderer.

  • Folder: Thermo‑Calc
  • File name: T_06_Serial_equilibrium_calculators.tcu

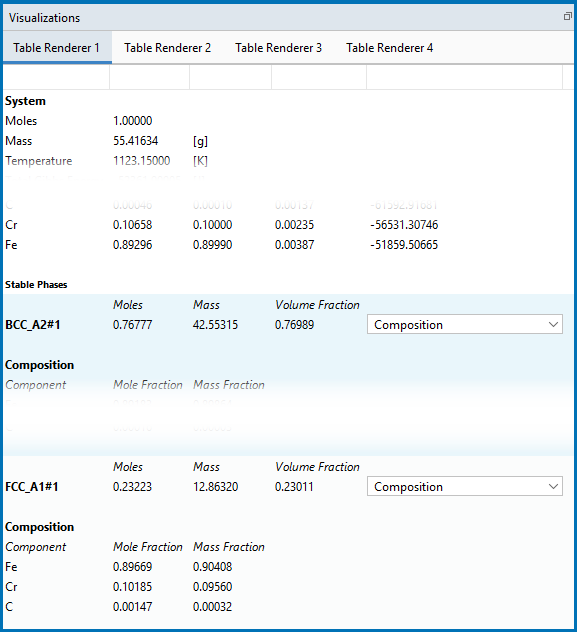
Table Renderer Results

This example is included as a tutorial on our website and as part of the Graphical Mode Examples playlist on our YouTube channel.

Open the example project file to review the node setup on the Project window and the associated settings on the Configuration window for each node. For some types of projects, you can also adjust settings on the Plot Renderer Configuration window to preview results before performing the simulation. Click Perform Tree to generate plots and tables to see the results on the Visualizations window.

In the first example, the objective is to calculate the equilibrium at 850° C where the mole fractions of the FCC A1 and BCC A2 phases are 0.5 each for an Fe-Cr-C steel with 10% chromium. In Equilibrium Calculator 1 a simple set of equilibrium conditions (temperature, pressure, system size and composition) are used to find a carbon content where only the FCC A1 and BCC A2 phases are stable. The results from this preliminary calculation are displayed in Table Renderer 1. Open the example to see the full table.

T_06 Preliminary results from Equilibrium Calculator 1

  • In Equilibrium Calculator 2 the carbon content equilibrium condition is replaced by the condition that the numbers of moles of the BCC A2 phase should be 0.5. The final result is displayed in Table Renderer 2. In this case, the final objective is to calculate the solidus temperature of an Fe-Cr-C steel with 10% Cr and 0.01% C.
  • In Equilibrium Calculator 3 the state at 2000 K is calculated and the result is displayed in Table Renderer 3.
  • In Equilibrium Calculator 4 the temperature equilibrium condition is replaced by the condition Fix phase / liquid / 0.0, meaning that liquid should be stable in an amount of zero moles, i.e. the solidus temperature. The final result is displayed in Table Renderer 4.